Bűvös lámpák

Az itt látható játékprogramban az a cél, hogy a megjelenő, kezdetben még nem látható (alvó) lámpák mindegyikét felkapcsoljuk. A kapcsolgatást egérkattintással végezhetjük. Ha egy lámpára kattintunk, akkor állapota megváltozik, de nem csak az övé, hanem minden lapszomszédjának állapota is.

Kezdetben megadhatjuk, hogy a lámpák hány sorban és hány oszlopban helyezkedjenek el. A sorok és oszlopok maximális száma 16.

A másik opció érdekesebb. Megadhatjuk, hogy a lámpák milyen felületen helyezkedjenek el. Lehet egy síkbeli téglalapon, vagy térben egy henger, vagy egy tórusz (úszógumi) felületén. Az utóbbiak a megjelenítésben nem láthatók, a működésben viszont igen. Úgy kell elképzelni a henger esetén, mintha az utolsó oszlop az első oszlop szomszédja lenne. Vagyis, ha az első oszlopon kattintunk, akkor annak az utolsó oszlopban is lesz hatása. A tórusznál pedig nemcsak az első oszlop és az utolsó oszlop szomszédos, hanem az első sor és az utolsó sor is.

Ha minden lámpát sikerült felkapcsolni, akkor a program írja ki: Game Over és ne engedje tovább a kapcsolgatást. A programból lehessen bármikor kilépni és bármikor új játékot kezdeni, valamint számolja, és írja ki a lépések számát a képernyőre.

A program egy futási képe:

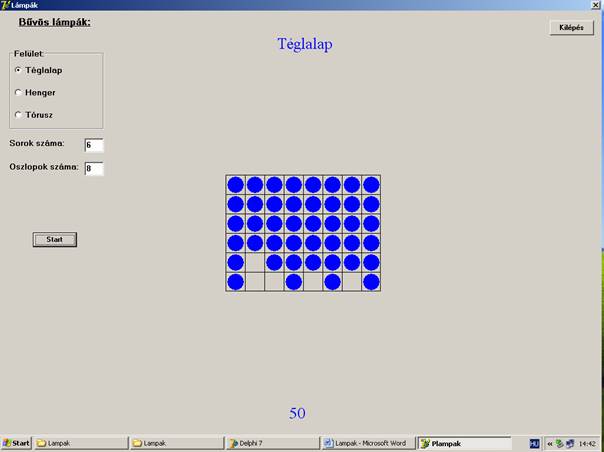
Ha sikerült felkapcsolni minden lámpát:

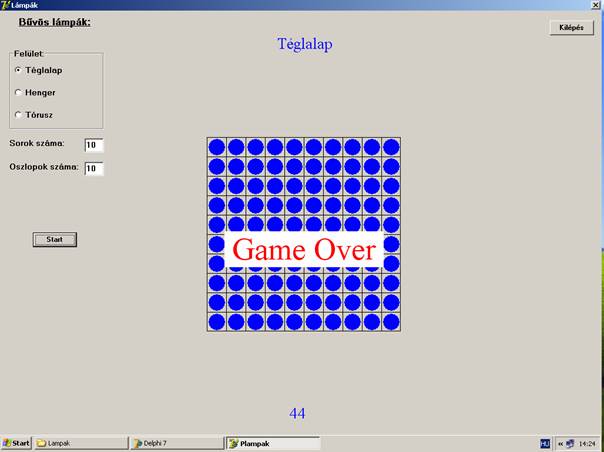
A program listája:

unit ULampak;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls, Grids;

type
  TfmLampak = class(TForm)
    btKilepes: TButton;
    btStart: TButton;
    lbLampak: TLabel;
    rgFelulet: TRadioGroup;
    lbSSz: TLabel;
    lbOSz: TLabel;
    edSSz: TEdit;
    edOSz: TEdit;
Procedure Racs(BFx,BFy,Bx,By,Nx,Ny: Integer);
Procedure Kepre;
Function Vege: Boolean;
procedure btKilepesClick(Sender: TObject);
procedure edSSzChange(Sender: TObject);
procedure edOSzChange(Sender: TObject);
procedure btStartClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormClick(Sender: TObject);
procedure FormMouseMove(Sender: TObject; Shift: TShiftState; X,
      Y: Integer);
procedure FormPaint(Sender: TObject);
procedure rgFeluletClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

Const Max=16;
      D=32;
      Dx=16;
      Dy=16;
      T=14;

var
  fmLampak: TfmLampak;
  Xk, Yk, Fx, Fy, Hx, Hy, Mx, My: Integer;
  L: Array[0..Max+1,0..Max+1] Of Byte;
  Felulet: Byte;
  F: Array[1..3] Of String;
  SSz, OSz: Byte;
  N: Word;
  VegeVan: Boolean;

implementation

{$R *.dfm}

procedure TfmLampak.btKilepesClick(Sender: TObject);
begin
  Close;
end;

procedure TfmLampak.FormPaint(Sender: TObject);
begin
With Canvas Do
Begin
    Pen.Color:= clBtnFace;
    Rectangle(Xk-80,35,Xk+80,80);
With Font Do
Begin
      Size:= 20;
      Name:= 'Times New Roman';
      Color:= clBlue;
End;
    TextOut(Xk-40,40,F[Felulet]);
    Pen.Color:= clBlack;
End;
end;

procedure TfmLampak.FormCreate(Sender: TObject);
begin
  Xk:= ClientWidth Div 2;
  Yk:= ClientHeight Div 2;
  F[1]:= 'Téglalap';
  F[2]:= 'Henger';
  F[3]:= 'Tórusz';
  Felulet:= 1;
  N:= 0;
VegeVan:= False;
end;

procedure TfmLampak.rgFeluletClick(Sender: TObject);
begin
  Felulet:= rgFelulet.ItemIndex+1;
  FormPaint(Sender);
  btStartClick(Sender);
end;

procedure TfmLampak.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
  Y: Integer);
begin
  Mx:= X;
  My:= Y;
If (Mx<Xk-(Fx-1)*D-1-Dx-T) Or (Mx>Xk+(Fx-1)*D+10+Dx+T) Or
     (My<Yk-(Fy-1)*D-1-Dy-T) Or (My>Yk+(Fy-1)*D+10+Dy+T) Then
  Cursor:= crDefault Else Cursor:= crCross;
end;

Procedure TfmLampak.Racs(BFx,BFy,Bx,By,Nx,Ny: Integer);
Var I, Sx,Sy: Integer;
Begin
If Nx*Ny=0 Then Exit;
  Sx:= Bfx+Nx*(Bx+1);
Sy:= Bfy+Ny*(By+1);
With Canvas Do
Begin
    Rectangle(BFx,Bfy,Sx,Sy);
    I:= BFx+Bx+1; While I<Sx Do
Begin MoveTo(I,BFy); LineTo(I,Sy); Inc(I,Bx+1) End;
    I:= BFy+By+1; While I<Sy Do
Begin MoveTo(BFx,I); LineTo(Sx,I); Inc(I,By+1) End;
End;
End;

procedure TfmLampak.edSSzChange(Sender: TObject);
begin
With edSSz Do
Begin
If Length(Text)>0 Then
If Not (Text[Length(Text)] In ['0'..'9']) Then Text:= '';
If Length(Text)>2 Then Text:= '';
End;
end;

procedure TfmLampak.edOSzChange(Sender: TObject);
begin
With edOSz Do
Begin
If Length(Text)>0 Then
If Not (Text[Length(Text)] In ['0'..'9']) Then Text:= '';
If Length(Text)>2 Then Text:= '';
End;
end;

procedure TfmLampak.btStartClick(Sender: TObject);
Var I, J: Word;
begin
  SSz:= StrToInt(edSSz.Text);
If SSz>Max Then Begin SSz:= Max; edSSz.Text:= IntToStr(SSz) End;
  OSz:= StrToInt(edOSz.Text);
If OSz>Max Then Begin OSz:= Max; edOSz.Text:= IntToStr(OSz) End;
  Fx:= Max Div 2;
  Fy:= Max Div 2;
With Canvas Do
Begin
    Pen.Color:= clBtnFace;
    Brush.Color:= clBtnFace;
    Rectangle(Xk-(Fx+1)*D,Yk-(Fy+1)*D,Xk+(Fx+1)*D,Yk+(Fy+1)*D);
    Pen.Color:= clBlack;
End;
Fx:= OSz Div 2;
  Fy:= SSz Div 2;
  Racs(Xk-Fx*D,Yk-Fy*D,D,D,OSz,SSz);
For I:= 0 To Max+1 Do For J:= 0 To Max+1 Do L[I,J]:= 0;
  FormPaint(Sender);
  N:= 0;
  VegeVan:= False;
end;

Procedure TfmLampak.Kepre;
Var I, J: Word;
Begin
With Canvas Do
For I:= 1 To OSz Do For J:= 1 To SSz Do
Begin
Case L[I,J] Of
      0: Begin
           Pen.Color:= clBtnFace;
           Brush.Color:= clBtnFace;
End;
      1: Begin
           Pen.Color:= clBlue;
           Brush.Color:= clBlue;
End;
End;
    Ellipse(Xk-(Fx-I)*D+I-Dx-T,Yk-(Fy-J)*D+J-Dy-T,
Xk-(Fx-I)*D+I-Dx+T,Yk-(Fy-J)*D+J-Dy+T);
    Pen.Color:= clBtnFace;
    Brush.Color:= clBtnFace;
    Rectangle(Xk-30,2*Yk-80,Xk+30,2*Yk);
    Pen.Color:= clBlue;
    TextOut(Xk-20,2*Yk-80,IntToStr(N));
    Pen.Color:= clBlack;
End;
End;

Function TfmLampak.Vege: Boolean;
Var I, J, S: Word;
Begin
  S:= 0; Vege:= False; VegeVan:= False;
For I:= 1 To OSz Do For J:= 1 To SSz Do Inc(S,L[I,J]);
If S=OSz*SSz Then With Canvas Do
Begin
With Font Do
Begin
      Size:= 40;
      Name:= 'Times New Roman';
      Color:= clRed;
End;
    Brush.Color:= clWhite;
TextOut(Xk-130,Yk,' Game Over ');
    Vege:= True; VegeVan:= True; N:= 0;
End;
End;

procedure TfmLampak.FormClick(Sender: TObject);
begin
If VegeVan Then Exit;
  Hx:= (Mx-Xk+(Fx+1)*D-OSz Div 2) Div D;
  Hy:= (My-Yk+(Fy+1)*D-SSz Div 2) Div D;
If (Hx<1) Or (Hx>OSz) Or (Hy<1) Or (Hy>SSz) Then Exit;
  Inc(N);
  L[Hx,Hy]:= 1-L[Hx,Hy];
  L[Hx-1,Hy]:= 1-L[Hx-1,Hy];
  L[Hx+1,Hy]:= 1-L[Hx+1,Hy];
  L[Hx,Hy-1]:= 1-L[Hx,Hy-1];
  L[Hx,Hy+1]:= 1-L[Hx,Hy+1];
If Felulet>1 Then
Begin
If Hx=1 Then L[OSz,Hy]:= 1-L[OSz,Hy];
If Hx=OSz Then L[1,Hy]:= 1-L[1,Hy];
End;
If Felulet>2 Then
Begin
If Hy=1 Then L[Hx,SSz]:= 1-L[Hx,SSz];
If Hy=SSz Then L[Hx,1]:= 1-L[Hx,1];
End;
  Kepre;
  Vege;
end;

end.