Latin négyzet (1. verzió)

A latin négyzet egy olyan N x N-es számtömb, melynek minden sorában és oszlopában pontosan egyszer fordul elő minden szám 1-től N-ig. Nevezhetjük véletlen latin négyzetnek azt a latin négyzetet, amelynek generálását a számítógép véletlen generátorára bíztuk. A jelen latin négyzet is ilyen.

Generálása úgy történik, hogy soronként haladva előállítja a számok egy véletlen permutációját, megnézi, hogy a felette lévőkkel nem ütközik-e, ha nem, akkor áttér a következő sorra, de ha elég sokszor próbálgatva nem talál megfelelőt, akkor sorokat törölve visszalép, és újra próbálkozik mindaddig, amíg az utolsó sor is jó nem lesz. Ez egy igen gyenge algoritmus, egy 10 x 10-e mező feltöltéséhez már több percnyi gépidő kell még egy gyors (2GHz, két magos) PC esetén is (de ez még mindig elfogadható sebesség, ahhoz képest, amit valaha a HT1080Z iskola-számítógép produkált, a maga 3 órájával). Ha az eredmény nem tetszik, vagy rendezgetni szeretnénk, akkor megtehetjük a jobb oldali beviteli mezők és nyomógombok segítségével (egyik beviteli mezőbe az egyik, a másikba a másik indexet kell írni, majd a megfelelő gombbal kiválasztjuk, hogy oszlopot, vagy sort akarunk cserélni). Mivel teljes sorokat és oszlopokat cserél, a latin-négyzet tulajdonság megmarad.

A program futási képe:

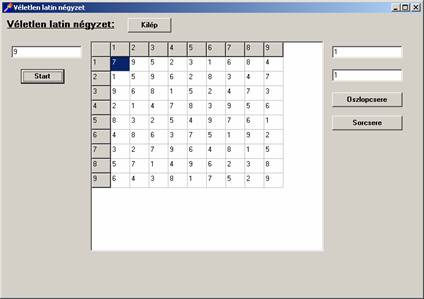
A program listája:

unit ULatin;

interface

uses
  Windows, Messages, SysUtils, Classes, 

Graphics, Controls, Forms, Dialogs, StdCtrls, Grids;

type
TfmLatin = class(TForm)
lbLatin: TLabel;
btKilep: TButton;
sgLatin: TStringGrid;
edN: TEdit;
edCsA: TEdit;
edCsB: TEdit;
btStart: TButton;
btOCsere: TButton;
btSCsere: TButton;
procedure btKilepClick(Sender: TObject);
procedure btStartClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure btOCsereClick(Sender: TObject);
procedure btSCsereClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

Const Max=100;

var
fmLatin: TfmLatin;
  N: Word;
  T: Array[1..Max,1..Max] Of Word;
  V, Vegso: Array[1..Max] Of Word;
Joe: Boolean;

implementation

{$R *.DFM}

Procedure Veletlen(N: Word);
Var Vl: Array[1..Max] Of Boolean;
    K,W: Word;
Begin
For K:= 1 To N Do Vl[K]:= False;
For K:= 1 To N Do
Begin
Repeat W:= Random(N)+1 Until Not Vl[W];
Vl[W]:= True; V[K]:= W;
End;
End;

Function Jo(N,M: Word): Boolean;
Var Lp: Boolean;
    K,L: Word;
Begin
Lp:= True; For K:= 1 To M-1 Do If Lp Then
For L:= 1 To N Do If V[L]=T[K,L] Then Lp:= False; Jo:= Lp;
End;

procedure TfmLatin.btKilepClick(Sender: TObject);
begin
Close;
end;

procedure TfmLatin.btStartClick(Sender: TObject);
Var I, J, S: Word;
begin
With sgLatin Do
Begin
    N:= StrToInt(edN.Text); ColCount:= N+1; RowCount:= N+1;
For I:= 1 To N Do
Begin Cells[I,0]:= IntToStr(I); Cells[0,I]:= IntToStr(I) End;
    I:= 0;
Repeat
      Inc(I);
If I=1 Then
Begin
Veletlen(N);
For J:= 1 To N Do Begin T[I,J]:= V[J]; Cells[J,I]:= IntToStr(V[J]) End;
End;
Joe:= False; S:= 0;
If I>1 Then
Repeat
Veletlen(N); For J:= 1 To N Do Cells[J,I]:= IntToStr(V[J]);
Joe:= Jo(N,I); Inc(S);
If S>10000*I Then Begin Dec(I,2); S:= 0 End;
Until Joe;
For J:= 1 To N Do T[I,J]:= V[J];
Until N=I;
End;
end;

procedure TfmLatin.FormCreate(Sender: TObject);
begin
Randomize;
end;

procedure TfmLatin.btOCsereClick(Sender: TObject);
Var A,B, I: Word;
    P: Array[1..Max] Of String;
begin
  A:= StrToInt(edCsA.Text);
  B:= StrToInt(edCsB.Text);
With sgLatin Do
Begin
For I:= 1 To N Do P[I]:= Cells[A,I];
For I:= 1 To N Do Cells[A,I]:= Cells[B,I];
For I:= 1 To N Do Cells[B,I]:= P[I];
End;
end;

procedure TfmLatin.btSCsereClick(Sender: TObject);
Var A,B, I: Word;
    P: Array[1..Max] Of String;
begin
  A:= StrToInt(edCsA.Text);
  B:= StrToInt(edCsB.Text);
With sgLatin Do
Begin
For I:= 1 To N Do P[I]:= Cells[I,A];
For I:= 1 To N Do Cells[I,A]:= Cells[I,B];
For I:= 1 To N Do Cells[I,B]:= P[I];
End;
end;

end.