Véletlen latin négyzetek kapcsolata
A honlap Latin négyzet szakaszának „Latin négyzet – cserélgetéssel” lapján nyitva hagytam azt a kérdést, hogyan készült az ottani programban a véletlen latin négyzet. Nem nehéz rá a válasz. A következő programképen a generálás első lépését láthatjuk:
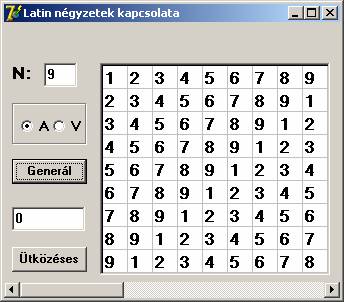
Ez egy nagyon speciális, ámbátor hibátlan latin négyzet, amely természetesen nem mondható véletlennek még a legjobb indulattal sem. Ha viszont megkeverjük, akkor már jogosnak tűnik a véletlen jelző:

A második tábla az elsőből úgy jött rétre, hogy teljes sorokat cserélgettünk teljes sorokkal, és teljes oszlopokat cserélgettünk teljes oszlopokkal, mindezt 1000-1000-szer, véletlen sor és oszlopválasztásokkal. A latin négyzet tulajdonság ugyanis invariáns a sorok illetve oszlopok egymás közti cseréjére. Nevezhetjük ezeket az átalakításokat elemi transzformációknak is.
Felmerült bennem a kérdés, vajon a véletlen latin négyzetek mind ilyenek-e, mindegyik így származtatható-e? Nem sokáig bizakodhattam a pozitív válaszban. A válasz ugyanis az, hogy nem.
Első lépésként azt vizsgáltam meg, hogy a fenti típusú négyzetből – nevezzem most jobb híján kvázi-véletlen latin négyzetnek – visszaállítható-e az alap, speciális latin négyzet. Ehhez a kvázi-véletlen latin négyzetet próbáltam véletlen elemi transzformációkkal visszaalakítani az alap latin négyzetre. A megvalósításban az ütközésmentesítő algoritmusom segített. Nézzük, mit kaptam:
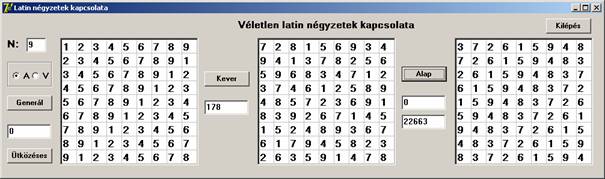
A fitness-függvény a mellékátlókban (bal alsó – jobb felső) elhelyezkedő elemek különbségének összegét számolja. A középső táblában ez az érték 178, mint látható. Az algoritmus 22663 ciklus alatt befejeződött, a fitness-érték 0 lett. Az alap latin négyzetet nem kaptuk vissza, már ez sem véletlen latin négyzet, még kvázi-véletlennek sem igazán mondható, hiszen a sorokban az első sornak mindig az eggyel balra eltolt permutációja látható. Az első sor nem a permutáció első eleme, hiszen nem a természetes sorrendben találhatók benne a számok. Próbálkozzunk újra a rendezéssel:
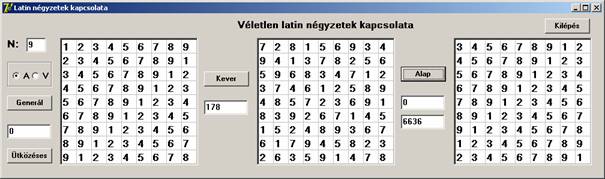
Most 6636 lépésben hajtotta végre a keresést, és most sem az alaptáblát kaptuk. Viszont elég egyszerű permutációt, hiszen egy 2-es eltolás csak a különbség az alap permutációhoz képest. Vajon mennyire véletlen ez. Tegyünk még egy próbát:
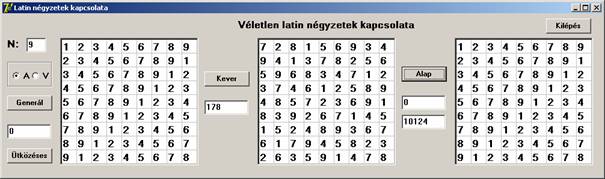
Most 10124 transzformációs lépés után visszakaptuk az alaptáblát. A keresést újra és újra végrehajtva ritkán előfordul, hogy az alaptáblát kapjuk. Volt olyan is, hogy az alaptábla teljes inverzióját (az első sor: 9,8,7,6, … 1 volt), de leginkább véletlen sorrendben voltak a számok az első sorban.
Mit mondhatunk ezek után a kvázi-véletlen latin négyzetekről. Azt, hogy gyakorlatilag csak egy latin négyzetről van szó, amelyet itt alapnak neveztem, ami ugye nem véletlen. Bármely kevert állapota visszaalakítható az alap négyzetté (triviálisan például úgy, hogy megjegyzem a cseréket, és visszafelé újra végrehajtom). Ha mégis csoportosítani szeretném őket, akkor 9! (n elemnél természetesen n!) csoportba sorolhatók, az első sor elemeit ugyanis ennyiféleképpen lehet a négyzetben elhelyezni, aztán a további sorokat eggyel-eggyel eltolni.
Eddig kiindulásként mindig az alap latin négyzetet választottuk. Induljunk ki most olyan latin négyzetből, amelyben az első sor nem a permutáció első eleme (nem a természetes sorrend), hanem eleve kevert állapotú („V” rádiógomb). Ugyanakkor most is az alap latin négyzetet keressük:
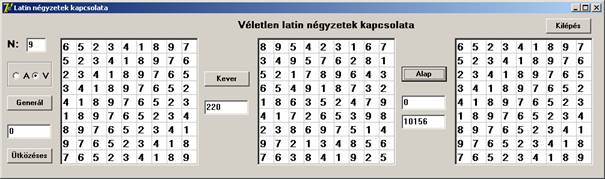
10156 lépés után megkaptuk a kiindulási négyzetet, de ez nem az alap négyzet. Próbálkozzunk tovább:
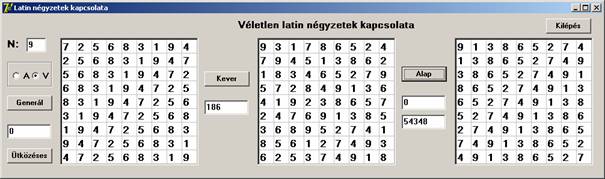
Most 54348 lépés után a kiindulási négyzet inverzét kaptuk. A számos próbálkozás egyike:
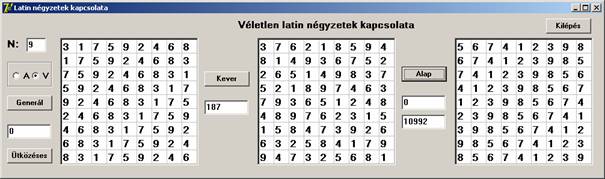
Legtöbbször sem az alap, sem a kiindulási négyzet közelébe sem jutunk. Keressünk alacsonyabb elemszámúak között:

Ötelemű négyzet esetén viszont kaptunk alap négyzetet is.
Eddig bízhattam abban, hogy valami módon a kvázi-véletlen latin négyzetet visszaszármaztathatom az alapra, hiszen a származása ezt sugallta. Ez többé-kevésbe így igaz. De mi a helyzet azokkal a latin négyzetekkel, amelyet nem a fenti alaptábla elemi transzformációk sorozatával jön létre, hanem soron és oszlopon belüli véletlen cserélgetéssel állítunk elő. Vajon ezekből elemi transzformációkkal kaphatunk-e kvázi-véletlen latin négyzeteket vagy nem. Próbálkozzunk először kisebb elemszámú (4) négyzetekkel:
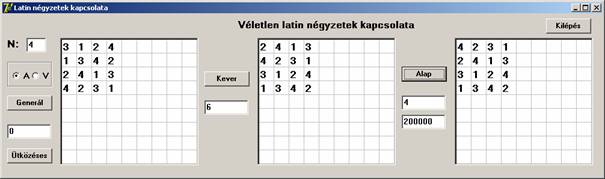
Az ütközésmentesítővel (Ütközéses gomb) generált táblát megkevertük, 6 hibapontos lett a kvázi-véletlen fitness-függvénye szerint. Megpróbálkoztunk az alap előállításával, de 200000 lépés után is maradt 4 hibapont. Minden valószínűség szerint ez a tábla teljesen független minden 4x4-es kvázi-véletlen latin négyzettől. Hasonló a helyzet a nagyobb négyzetek esetén is. Csak nagyon ritkán fordulhat elő, hogy egy így generált véletlen latin négyzetnek kvázi-véletlen alapja lenne. Nézzük egy nagyobb táblát is:
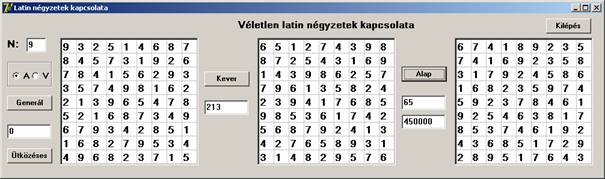
Itt a kezdeti fitness érték 213 volt, melyet az algoritmus 450000 lépésben 65-re csökkentett. Megfigyelhető az eredménytáblában a rendezettség. Az 1-es teljesen rendezett, a 2-esnél két hiba van, a többi számnál még ennél is több.
Ha újra a kisebb táblák felé fordulunk és megpróbálunk Ütközésmentesítővel előállított táblák között kvázi-véletlent keresni, nem kell túl sokszor próbálkoznunk:
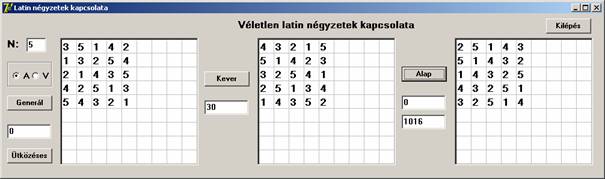
Ez egy 30-as fitness értékű tábla volt, melyhez az algoritmus 1016 lépésben megtalálta a kvázi-véletlen alaptáblát. Ennek az lehet az oka, hogy az alacsony elemszám miatt nagyobb valószínűséggel tudunk előállítani ilyen táblákat, mint nagy elemszámú latin négyzetek esetén. Ha viszont az elemszámnak például 3-at választunk, akkor minden latin négyzet egyben kvázi-véletlen lesz:
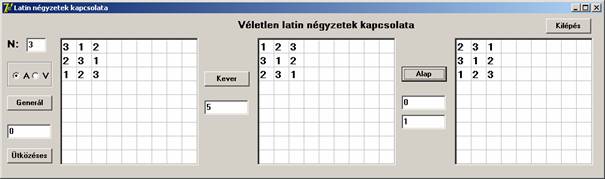
A program listája:
unit UALatin;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids, ExtCtrls;
Const Max=9;
type
TfmALatin = class(TForm)
btKilepes: TButton;
lbVLN: TLabel;
btGeneral: TButton;
sgVeletlen: TStringGrid;
btAlap: TButton;
sgAlap: TStringGrid;
edUtkozes: TEdit;
edUUtkozes: TEdit;
edN: TEdit;
sgKevert: TStringGrid;
btKever: TButton;
edKevert: TEdit;
rgAV: TRadioGroup;
btUtkozeses: TButton;
lbN: TLabel;
edMM: TEdit;
Procedure GKepre;
Procedure KKepre;
Procedure AKepre;
Function Utkoz: Word;
Function UUtkoz: Word;
Procedure SCsere(A, B: Word);
Procedure OCsere(A, B: Word);
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure btGeneralClick(Sender: TObject);
procedure btAlapClick(Sender: TObject);
procedure btKeverClick(Sender: TObject);
procedure btUtkozesesClick(Sender: TObject);
procedure edMMChange(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
fmALatin: TfmALatin;
GLat, KLat, PLat, ALat, ULat, LLat: Array[1..Max,1..Max] Of Word;
SorA, SorP: Array[1..Max] Of Word;
MM: Word;
implementation
{$R *.dfm}
procedure TfmALatin.btKilepesClick(Sender: TObject);
begin
Close;
end;
procedure TfmALatin.FormCreate(Sender: TObject);
begin
Randomize;
With sgVeletlen Do
Begin
ColWidths[0]:= 0;
RowHeights[0]:= 0;
ColWidths[ColCount-1]:= 0;
RowHeights[RowCount-1]:= 0;
Col:= ColCount-1;
Row:= RowCount-1;
End;
With sgKevert Do
Begin
ColWidths[0]:= 0;
RowHeights[0]:= 0;
ColWidths[ColCount-1]:= 0;
RowHeights[RowCount-1]:= 0;
Col:= ColCount-1;
Row:= RowCount-1;
End;
With sgAlap Do
Begin
ColWidths[0]:= 0;
RowHeights[0]:= 0;
ColWidths[ColCount-1]:= 0;
RowHeights[RowCount-1]:= 0;
Col:= ColCount-1;
Row:= RowCount-1;
End;
edMM.Text:= IntToStr(Max); MM:= Max;
end;
procedure TfmALatin.edMMChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edMM.Text,MM,Kod);
end;
Procedure TfmALatin.GKepre;
Var I, J: Word;
Begin
With sgVeletlen Do For J:= 1 To MM Do For I:= 1 To MM Do
Cells[I,J]:= IntToStr(GLat[J,I]);
End;
Procedure TfmALatin.KKepre;
Var I, J: Word;
Begin
With sgKevert Do For J:= 1 To MM Do For I:= 1 To MM Do
Cells[I,J]:= IntToStr(KLat[J,I]);
End;
Procedure TfmALatin.AKepre;
Var I, J: Word;
Begin
With sgAlap Do For J:= 1 To MM Do For I:= 1 To MM Do
Cells[I,J]:= IntToStr(ALat[J,I]);
End;
Function TfmALatin.Utkoz: Word;
Var I, J, U: Word;
Begin
U:= 0; For I:= 1 To MM-1 Do For J:= 2 To MM Do
U:= U+Abs(ULat[I,J]-ULat[I+1,J-1]); Utkoz:= U;
End;
Function TfmALatin.UUtkoz: Word;
Var I, J, K, U: Word;
Begin
U:= 0; For I:= 1 To MM Do For J:= 1 To MM Do For K:= 1 To MM Do
If (K<>J) And (ULat[J,I]=ULat[K,I]) Then Inc(U); UUtkoz:= U;
End;
Procedure TfmALatin.SCsere(A, B: Word);
Var I: Word;
P: Array[1..Max] Of Word;
Begin
For I:= 1 To MM Do P[I]:= ULat[A,I];
For I:= 1 To MM Do ULat[A,I]:= ULat[B,I];
For I:= 1 To MM Do ULat[B,I]:= P[I];
End;
Procedure TfmALatin.OCsere(A, B: Word);
Var I: Word;
P: Array[1..Max] Of Word;
Begin
For I:= 1 To MM Do P[I]:= ULat[I,A];
For I:= 1 To MM Do ULat[I,A]:= ULat[I,B];
For I:= 1 To MM Do ULat[I,B]:= P[I];
End;
procedure TfmALatin.btGeneralClick(Sender: TObject);
Var A, B, I, J, P: Word;
begin
With sgVeletlen Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
For I:= 1 To MM Do GLat[I,1]:= I;
If rgAV.ItemIndex=1 Then
For J:= 1 To 500 Do
Begin
A:= Random(MM)+1; B:= Random(MM)+1;
P:= GLat[A,1]; GLat[A,1]:= GLat[B,1]; GLat[B,1]:= P;
End;
For J:= 2 To MM Do
Begin
For I:= 1 To MM-1 Do GLat[I,J]:= GLat[I+1,J-1];
GLat[MM,J]:= GLat[1,J-1];
End;
ULat:= GLat;
edUtkozes.Text:= IntToStr(Utkoz);
GKepre;
With sgKevert Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
With sgAlap Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
KLat:= GLat;
KKepre; edKevert.Text:= '0';
end;
procedure TfmALatin.btUtkozesesClick(Sender: TObject);
Var I, J, A, B, P, S, UH: Word;
H: Integer;
N: LongInt;
begin
edN.Text:= '0'; edN.Repaint;
With sgVeletlen Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
sgVeletlen.Repaint;
With sgKevert Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
sgKevert.Repaint;
For I:= 1 To MM Do For J:= 1 To MM Do GLat[I,J]:= J;
For I:= 1 To MM Do For J:= 1 To 100 Do
Begin
A:= Random(MM)+1; B:= Random(MM)+1;
P:= GLat[I,A]; GLat[I,A]:= GLat[I,B]; GLat[I,B]:= P;
End;
ULat:= GLat; H:= MaxInt; N:= 0;
While (H>0) And (N<1000) Do
Begin
H:= UUtkoz; edUtkozes.Text:=IntToStr(UUtkoz); edUtkozes.Repaint;
S:= Random(MM)+1; A:= Random(MM)+1; B:= Random(MM)+1;
P:= ULat[S,A]; ULat[S,A]:= ULat[S,B]; ULat[S,B]:= P;
UH:= UUtkoz;
If UH>H Then
Begin
UH:= H; edUtkozes.Text:= IntToStr(UH); edUtkozes.Repaint;
P:= ULat[S,A]; ULat[S,A]:= ULat[S,B]; ULat[S,B]:= P;
End;
End;
edUtkozes.Text:= IntToStr(UUtkoz); GLat:= ULat;
GKepre; edUtkozes.Text:= IntToStr(H);
KLat:= GLat;
KKepre; edKevert.Text:= IntToStr(Utkoz);
With sgAlap Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
end;
procedure TfmALatin.btKeverClick(Sender: TObject);
Var A, B, I, J: Word;
begin
KLat:= GLat;
For I:= 1 To 1000 Do
Begin
A:= Random(MM)+1; B:= Random(MM)+1;
For J:= 1 To MM Do SorP[J]:= KLat[A,J];
For J:= 1 To MM Do KLat[A,J]:= KLat[B,J];
For J:= 1 To MM Do KLat[B,J]:= SorP[J];
A:= Random(MM)+1; B:= Random(MM)+1;
For J:= 1 To MM Do SorP[J]:= KLat[J,A];
For J:= 1 To MM Do KLat[J,A]:= KLat[J,B];
For J:= 1 To MM Do KLat[J,B]:= SorP[J];
End;
ULat:= KLat;
edKevert.Text:= IntToStr(Utkoz);
With sgAlap Do For I:= 1 To Max Do For J:= 1 To Max Do Cells[I,J]:= '';
edUUtkozes.Text:= '0';
edN.Text:= '0';
KKepre;
end;
procedure TfmALatin.btAlapClick(Sender: TObject);
Var X, Y, UH: Word;
H, PH: Integer;
N, M: LongInt;
begin
ULat:= KLat; PLat:= KLat; LLat:= KLat;
H:= MaxInt; PH:= MaxInt; N:= 0; M:= 0;
edN.Text:= '0'; edN.Repaint;
While (H>0) And (N<50000*MM) Do
Begin
Inc(N); Inc(M);
If N Mod 5000=0 Then Begin edN.Text:= IntToStr(N); edN.Repaint End;
H:= Utkoz; X:= Random(MM)+1; Y:= Random(MM)+1; SCsere(X,Y);
UH:= Utkoz; If UH>H Then SCsere(X,Y) Else
Begin
UH:= H; edUUtkozes.Text:= IntToStr(UH); edUUtkozes.Repaint;
ALat:= ULat; AKepre; sgAlap.Repaint;
If UH<=PH Then Begin PH:= UH; LLat:= ULat End;
End;
H:= Utkoz; X:= Random(MM)+1; Y:= Random(MM)+1; OCsere(X,Y);
UH:= Utkoz; If UH>H Then OCsere(X,Y) Else
Begin
UH:= H; edUUtkozes.Text:= IntToStr(UH); edUUtkozes.Repaint;
ALat:= ULat; AKepre; sgAlap.Repaint;
If UH<=PH Then Begin PH:= UH; LLat:= ULat End;
End;
If (H>0) And (M>50*MM) Then
Begin ULat:= PLat; M:= 0 End;
End;
If H>0 Then Begin H:= PH; ALat:= LLat End Else ALat:= ULat; AKepre;
edUUtkozes.Text:= IntToStr(H); EdN.Text:= IntToStr(N);
end;
end.