Vezérek elhelyezése sakktáblán Genetikus algoritmussal

A genetikus algoritmusoknak ott nagy a létjogosultsága, ahol a feladatok megoldását nagyon magas elemszámú állapottérből kell megkeresni. Ekkor a fentebb (előző vezér-elhelyezési programokban) is használt keresési eljárások a gépek korlátozott sebessége miatt nem használható.

Mint láttuk, vannak olyan reprezentációi a kitűzött feladatnak, melyek egész hamar megoldásra vezetnek. Ezek a reprezentációk már önmagukban hordozzák a feladat specifikus tulajdonságait, így az állapottér elemszáma értelmes méretekre csökkenthető volt.

Ebben a szakaszban mintegy elfelejtve az imént említett reprezentációkat, úgy tekintünk a feladatra, mintha az elemi tulajdonságait nem ismernénk, azt csak az algoritmus közben, az egyedek jóságának vizsgálatakor érvényesítjük. Így az egyedek a populációk során válnak külön-külön a jó tulajdonságok hordozóivá.

A Genetikus algoritmus lényege az, hogy kezdetben véletlenül megválasztott elemekből létrehozunk egy populációt (genetikus kódot, elrendezést, az elemszámot a feladat maga, illetve a rendelkezésre álló erőforrás erősen befolyásolja). Majd a következő populációt (generációt) az előzőből például keresztezéssel és/vagy mutációval létrehozzuk. A keresztezés azt jelenti, hogy két egyed genetikus kódját részben kicseréljük, így új egyedeket hozunk létre. A mutációnál az egyes egyed genetikus kódját véletlen módon megváltoztatjuk.

A keresztezésnél az a cél, hogy azon egyedek kódja öröklődjenek, amelyek jók. Tehát két jónak minősített egyedet keresztezünk, és két rossznak (gyengének) mutatkozó egyed helyett ezek fognak szerepelni a következő populációban. Így elvileg a populáció egyre jobb tulajdonságú elemekből fog állni. Azt várjuk, hogy keresztezés révén a populációban elő fog fordulni legalább egy, a lehető legjobb tulajdonságokkal rendelkező egyed, ami a feladat megoldását jelenti. Ez persze általában nem így van. Ha az egyedek összességében nem hordozzák a legjobb megoldás kódját, akkor nem kapjuk meg a feladat megoldását. Ekkor az egyedek jósága egy bizonyos szint fölé nem fog emelkedni és szükség lesz a mutációra.

Mutációt akkor kell alkalmazni, amikor a populáció jósága egy szinten (de nem a tökéletes megoldást jelentőn) megakad, azaz keresztezéssel már nem képes tovább fejlődni. Ekkor az egyedek genetikus kódját egy adott százalékos valószínűséggel, véletlen értékre változtatjuk, azaz a kódot frissítjük. Ettől azt várjuk, hogy a holtponti helyzetből a populáció kimozdul, lesznek újra rossz és jó tulajdonságú egyedek, és reményeink szerint a véletlen választás folytán előáll a legjobb tulajdonságú egyed előállítására alkalmas genetikai kód is. Általában igaz, hogy a mutációt nem túl magas százalékban kell alkalmazni, különben a már felhalmozódott jó tulajdonságok eltűnnek az egyedekből.

Az itt leírtak szerint készült a címben megfogalmazott feladatra a program. A programnak nem az a célja, hogy az előző feladatokban látható megoldások felett győzedelmeskedjen. Az összes lehetséges elhelyezést megadó programon egyébként már nincs mit javítani, az pillanatok alatt mindent elmond a problémáról. A cél tehát a genetikus algoritmus bemutatása egy viszonylag egyszerű, más eszközökkel is megoldott problémára. A program listája szerintem megfelelően kommentezett, így magyarázatra nem szorul.

A program futási képei. Induláskor:

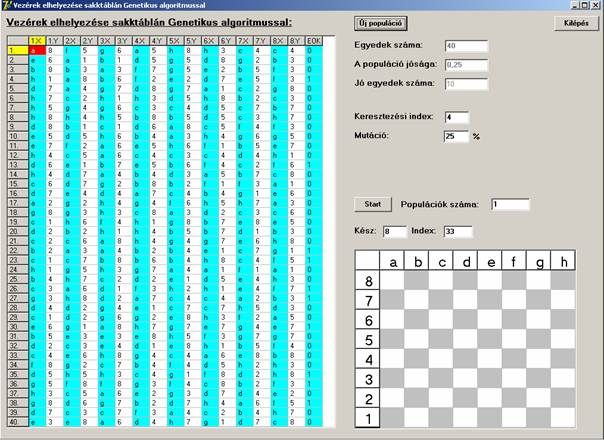
A keresés végén:

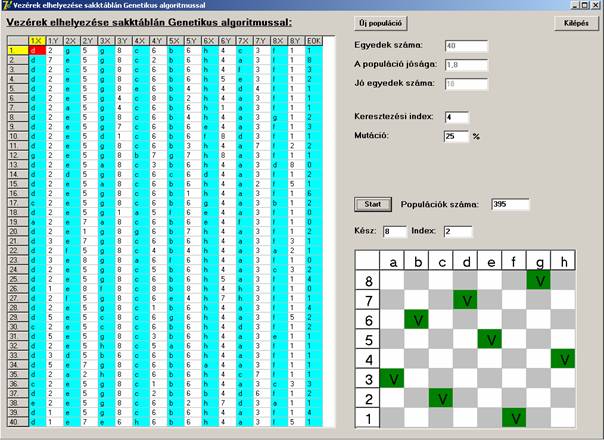
A program listája.

unit UGenVezer;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls, Grids;

Const EgyedSz=40;
      Max=8;
type
  TfmGenVezer = class(TForm)
    lbHenVezer: TLabel;
    btKilepes: TButton;
    sgGenVezer: TStringGrid;
    btUjPop: TButton;
    sgTabla: TStringGrid;
    lbJosag: TLabel;
    edJosag: TEdit;
    lbEgyedSz: TLabel;
    edEgyedSz: TEdit;
    lbJokSz: TLabel;
    edJokSz: TEdit;
    btStart: TButton;
    lbPopSz: TLabel;
    edPSz: TEdit;
    lbKesz: TLabel;
    edKesz: TEdit;
    lbIndex: TLabel;
    edIndex: TEdit;
    lbMutacio: TLabel;
    edMutacio: TEdit;
    lbSzazalek: TLabel;
lbKereszt: TLabel;
    edKereszt: TEdit;
Procedure PopInit;
Procedure Vizsgal;
Procedure PopKepre;
Procedure Tablara(Ind: Word);
Procedure Keresztez;
Procedure Mutacio;
procedure FormCreate(Sender: TObject);
procedure btKilepesClick(Sender: TObject);
procedure sgGenVezerDrawCell(Sender: TObject; Col, Row: Integer;
      Rect: TRect; State: TGridDrawState);
procedure sgGenVezerClick(Sender: TObject);
procedure btUjPopClick(Sender: TObject);
procedure sgTablaDrawCell(Sender: TObject; Col, Row: Integer;
      Rect: TRect; State: TGridDrawState);
procedure btStartClick(Sender: TObject);
procedure edMutacioChange(Sender: TObject);
procedure edKeresztChange(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

  THely=Record
    X, Y: Byte;
    Jo: Boolean;      //true, ha a vezér nincs ütésben
End;

  TEgyed=Record
    EXY: Array[1..Max] Of THely;
    EOK: Byte;        //az ütésben nem álló vezérek száma
    JoEgyed: Boolean; //true, ha az ütésben nem álló vezérek szám átlag feletti
End;

var
  fmGenVezer: TfmGenVezer;
  ACol, ARow: Integer;
Colors: Array[1..Max,1..Max] Of Boolean;
  EgyedT: Array[1..EgyedSz] Of TEgyed;
  JokSz: Word;        //az átlag feletti egyedek száma
  Josag: Real;        //a populáció ütésben nem álló vezéreinek átlaga
  Kereszt: Byte;      //a keresztezési index
  Uj1, Uj2: TEgyed;   //új egyedek
  IR1, IR2, IJ1, IJ2: Word;  //régi és új egyedek tömbindexei
  PSz: Word;                 //populációk száma
  OKMax, IMax, OldMax, //segédváltozók a populációk generálásánál
  MutSz: Word;         //mutáció erősségét mutató százalékérték

implementation

{$R *.dfm}

procedure TfmGenVezer.btKilepesClick(Sender: TObject);
begin
//kilépés a programból
  Close;
end;

procedure TfmGenVezer.sgGenVezerClick(Sender: TObject);
begin
//kattintás után az egyed megjelenítése a képernyőn lévő sakktáblán
  PopKepre;
With sgGenVezer Do Begin ACol:= Col; ARow:= Row; RePaint End;
  Tablara(ARow);
end;

procedure TfmGenVezer.sgGenVezerDrawCell(Sender: TObject; Col,
  Row: Integer; Rect: TRect; State: TGridDrawState);
begin
//a populációt megjelenítő StringGrid beállításai
With sgGenVezer.Canvas.Brush Do
Begin
{rögzített cellák}
If (gdFixed In State) And ((Col=ACol) Or (Row=ARow)) Then
    Color:= clYellow Else Color:=clBtnFace;

{kiválasztott cella}
If gdSelected In State Then Color:= clRed;

{a táblázat belseje}
If Not((gdSelected In State) Or (gdFixed In State)) Then
If Odd(Col) Then Color:= clAqua Else Color:= clWindow;
End;
  sgGenVezer.Canvas.TextRect(Rect,Rect.Left+3,Rect.Top+1,
                             sgGenVezer.Cells[Col,Row]);
If gdFocused In State Then sgGenVezer.Canvas.DrawFocusRect(Rect);
end;

procedure TfmGenVezer.sgTablaDrawCell(Sender: TObject; Col, Row: Integer;
Rect: TRect; State: TGridDrawState);
begin
//a sakktáblát és felállást megjelenítő StringGrid beállításai
With sgTabla.Canvas.Brush Do
Begin
{rögzített cellák}
If gdFixed In State Then Color:=clWhite;

{kiválasztott cella}
If gdSelected In State Then Color:= clSilver;

{a táblázat belseje}
If Not((gdSelected In State) Or (gdFixed In State)) Then
Begin
Case Odd(Col) XOr Odd(Row) Of
        False: Color:= clWindow;
        True: Color:= clSilver;
End;
If Colors[Col,Row] Then Color:= clGreen;
End;
    sgTabla.Canvas.Font.Size:= 17;
End;
sgTabla.Canvas.TextRect(Rect,Rect.Left+16,
                          Rect.Top+4,sgTabla.Cells[Col,Row]);
If gdFocused In State Then sgTabla.Canvas.DrawFocusRect(Rect);
end;

procedure TfmGenVezer.edKeresztChange(Sender: TObject);
Var Kod: Integer;
begin
  Val(edKereszt.Text, Kereszt, Kod);
end;

procedure TfmGenVezer.edMutacioChange(Sender: TObject);
Var Kod: Integer;
begin
  Val(edMutacio.Text, MutSz, Kod);
end;

Procedure TfmGenVezer.PopInit;
Var I, J: Word;
Begin
//egy teljes populáció létrehozása
For I:= 1 To EgyedSz Do With EgyedT[I] Do
Begin
For J:= 1 To Max Do With EXY[J] Do
Begin
      X:= Random(Max)+1;
      Y:= Random(Max)+1;
      Jo:= True;
End;
    EOK:= 0;
    JoEgyed:= False;
End;
End;

Procedure TfmGenVezer.Vizsgal;
Var I, J, K, Sz: Word;
    Utesben: Boolean;
Begin
//a populáció vizsgálata
//megállapítja minden vezérről, hogy ütésben van-e (-> Utesben)
//megállapítja minden egyedről, hogy hány vezér elhelyezkedése jó (-> Jo)
  JokSz:= 0; OKMax:= 0;
For I:= 1 To EgyedSz Do With EgyedT[I] Do
Begin
    Sz:= 0;
For J:= 1 To Max Do
Begin
      Utesben:= False; For K:= 1 To Max Do If J<>K Then
If EXY[J].X=EXY[K].X Then Begin Utesben:= True; Break End;
If Not Utesben Then For K:= 1 To Max Do If J<>K Then
If EXY[J].Y=EXY[K].Y Then Begin Utesben:= True; Break End;
If Not Utesben Then For K:= 1 To Max Do If J<>K Then
If Abs(EXY[J].X-EXY[K].X)=Abs(EXY[J].Y-EXY[K].Y) Then
Begin Utesben:= True; Break End;
      EXY[J].Jo:= Not Utesben;
If Not Utesben Then Inc(Sz);
End;
    EOK:= Sz; If EOK>OKMax Then Begin OKMax:= EOK; IMax:= I End;
    Inc(JokSz,EOK);
End;
//megállapítja a populáció jóságát:
//jó helyezetű vezérek számának átlaga-> Josag
Josag:= JokSz/EgyedSz;
  edJosag.Text:= FloatToStr(Josag);
//minden egyedről megállapítja, hogy jó-e:
//átlag feletti a jó helyzetű vezérek száma -> JoEgyed:= True
  JokSz:= 0;
For I:= 1 To EgyedSz Do With EgyedT[I] Do If EOK>Josag Then
Begin
    Inc(JokSz);
    JoEgyed:= True;
End Else JoEgyed:= False;
  edJokSz.Text:= IntToStr(JokSz);
End;

Procedure TfmGenVezer.Keresztez;
Var I, V, R: Word;
Begin
  Inc(PSz);
//a két legrosszabb egyed keresése
  V:= Random(EgyedSz)+1; R:= Max; IR1:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do
If Not JoEgyed And (EOK<R) Then Begin R:= EOK; IR1:= I End;
For I:= 1 To V  Do With EgyedT[I] Do
If Not JoEgyed And (EOK<R) Then Begin R:= EOK; IR1:= I End;

  V:= Random(EgyedSz)+1; R:= Max; IR2:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do If I<>IR1 Then
If Not JoEgyed And (EOK<R)Then Begin R:= EOK; IR2:= I End;
For I:= 1 To V  Do With EgyedT[I] Do If I<>IR1 Then
If Not JoEgyed And (EOK<R) Then Begin R:= EOK; IR2:= I End;

//két jó egyed keresése:
//nem a két legjobbat, mert akkor nem lenne eléggé nagy a változatosság
  V:= Random(EgyedSz)+1; IJ1:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do If JoEgyed Then IJ1:= I;
For I:= 1 To V  Do With EgyedT[I] Do If JoEgyed Then IJ1:= I;

  V:= Random(EgyedSz)+1; IJ2:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do If I<>IJ1 Then
If JoEgyed Then IJ2:= I;
For I:= 1 To V  Do With EgyedT[I] Do If I<>IJ1 Then
If JoEgyed Then IJ2:= I;

//két jó egyed keresztezése -> Uj1, Uj2: TEgyed
If IJ1*IJ2<>0 Then
Begin
For I:= 1 To Kereszt Do Uj1.EXY[I]:= EgyedT[IJ1].EXY[I];
For I:= Kereszt+1 To Max Do Uj1.EXY[I]:= EgyedT[IJ2].EXY[I];
    Uj1.JoEgyed:= False;
For I:= 1 To Kereszt Do Uj2.EXY[I]:= EgyedT[IJ2].EXY[I];
For I:= Kereszt+1 To Max Do Uj2.EXY[I]:= EgyedT[IJ1].EXY[I];
    Uj2.JoEgyed:= False;
End;
End;

Procedure TfmGenVezer.Mutacio;
Var I, J: Word;
Begin
//a populáció minden egyedének mindkét koordinátáját MutSz valószínűséggel
//módosítjuk egy véletlen értékr
For I:= 1 To EgyedSz Do With EgyedT[I] Do
For J:= 1 To Max Do With EXY[J] Do
Begin
If Random(100)<MutSz Then X:= Random(Max)+1;
If Random(100)<MutSz Then Y:= Random(Max)+1;
End;
End;

procedure TfmGenVezer.btStartClick(Sender: TObject);
begin
//populációk generálása és vizsgálata
  OKMax:= 0; IMax:= 0; PSz:= 0;
Repeat
    OldMax:= OKMax;
    Keresztez;
If JokSz In [2,3,4] Then Mutacio;
If (IR1*IR2<>0) And (IJ1*IJ2<>0) Then
Begin
      EgyedT[IR1]:= Uj1;
      EgyedT[IR2]:= Uj2;
End
Else Mutacio;
    Vizsgal;
    PopKepre;
    edPSz.Repaint;
If OKMax>OldMax Then
Begin
      sgGenVezer.Repaint;
      edKesz.Text:= IntToStr(OKMax); edKesz.Repaint;
      edIndex.Text:= IntToStr(IMax); edIndex.Repaint;
      Tablara(IMax); sgTabla.Repaint;
End;
Until (OKMax>=Max) Or (PSz>20000);
//max értékig, vagy maximum 20000 permutációig keresünk

end;

Procedure TfmGenVezer.PopKepre;
Var I, J: Word;
Begin
//a populáció minden egyedét, a jó elhelyezkedésü vezérek számával együtt
//megjeleníti egy StringGrid-ben
With sgGenVezer Do
Begin
For I:= 1 To EgyedSz Do With EgyedT[I] Do
Begin
For J:= 1 To Max Do With EXY[J] Do
Begin
        Cells[2*J-1,I]:= Char(96+X);
        Cells[2*J  ,I]:= IntToStr(Y);
End;
      Cells[ColCount-1,I]:= IntToStr(EOK);
End;
End;
  edPSz.Text:= IntToStr(PSz);
End;

Procedure TfmGenVezer.Tablara(Ind: Word);
Var I, J: Word;
Begin
//egy egyed megjelenítés a sakktáblán
With sgTabla Do
Begin
For I:= 1 To ColCount-1 Do For J:= 1 To RowCount-1 Do Cells[I,J]:= '';
For I:=1 To Max Do For J:= 1 To Max Do Colors[I,J]:= False;
With EgyedT[Ind] Do For I:= 1 To Max Do With EXY[I] Do
Begin
      Cells[X,Max-Y+1]:= 'V';
      Colors[X,Max-Y+1]:= Jo;
End;
End;
  sgTabla.Repaint;
End;

procedure TfmGenVezer.FormCreate(Sender: TObject);
Var I: Word;
    Ch: Char;
begin
//a program vízuális elemeinek megjelenítése, a kezdeti populáció generálása
  ACol:= 1; ARow:= 1;
With sgGenVezer Do
Begin
    RowCount:= EgyedSz+1;
    ColWidths[0]:= 35;
For I:= 1 To RowCount-1 Do Cells[0,I]:= IntToStr(I)+'.';
For I:= 1 To Max Do
Begin
      Cells[2*I-1,0]:= IntToStr(I)+'.X';
      Cells[2*I  ,0]:= IntToStr(I)+'.Y';
End;
    Cells[ColCount-1,0]:= 'EOK';
End;

With sgTabla Do
Begin
    ColWidths[9]:= 0;
    RowHeights[9]:= 0;
For I:= 1 To 8 Do Cells[0,I]:= IntToStr(9-I);
For Ch:= 'a' To 'h' Do Cells[Ord(Ch)-96,0]:= Ch;
    Col:= 9; Row:= 9;
End;

  Randomize;
  PopInit;
  Vizsgal;
  PopKepre;

//kezdő és alapértelmezett értékek:
edEgyedSz.Text:= IntToStr(EgyedSz);
  PSz:= 1; edPSz.Text:= IntToStr(PSz);
  MutSz:= 25; edMutacio.Text:= IntToStr(MutSz);
  Kereszt:= 4; edKereszt.Text:= IntToStr(Kereszt);

end;

procedure TfmGenVezer.btUjPopClick(Sender: TObject);
Var I, J: Word;
begin
//új populáció generálása
For I:= 1 To Max Do For J:= 1 To Max Do Colors[I,J]:= False;
With sgTabla Do
For I:= 1 To ColCount-1 Do For J:= 1 To RowCount-1 Do Cells[I,J]:= '';
  PopInit;
  Vizsgal;
  PopKepre;
  PSz:= 1; edPSz.Text:= IntToStr(PSz);
end;

end.