Az utazó ügynök problémájának megoldása egyidejűleg ütközésmentesítő és genetikus algoritmussal

Már számos probléma megoldásában jó szolgálatot tett az általam ütközésmentesítőnek nevezett algoritmus. Meg kell viszont állapítanom, hogy ezek eddig mind olyan problémák voltak, amelyeknek a megoldottsága egyértelmű volt. Azaz a megoldás nulla hibapontos eredmények elérésével jött létre. Ilyenek voltak:

- nyolc vezér elhelyezése sakktáblán ütközésmentesen,

- a torpedó játék játéktere,

- latin négyzetek előállítása,

- fakocka kirakó,

- órarendkészítő program,

- sudoku táblák készítése.

Ezen a lapon olyan feladat megoldását találjuk – az utazó ügynök problémáját – amely megoldása során nem látható minden kétséget kizáróan, hogy a problémát a lehető legjobban oldottuk meg. Csak azt tudjuk majd mondani, hogy ennyi vagy annyi gépi idő alatt, milyen végeredményhez jutottunk. Senki és semmi nem tudja majd azt állítani, hogy van vagy nincs jobb megoldás az általunk előállítottnál.

A szakirodalomban számos helyen találunk leírást a probléma genetikus algoritmussal történő megoldására. Arra gondoltam, hogy az ütközésmentesítő algoritmusommal mintegy versenyeztetni kellene a genetikus algoritmust. Így további megerősítést kaphatnánk arra vonatkozóan, hogy mennyire hatékony (vagy nem) az ütközésmentesítő algoritmus. Az az ötletem támadt, hogy a két algoritmusnak készítsünk Delphi-ben egy-egy szálat, induljon ugyanazon kezdeti paraméterekkel a keresés, és nézzük meg, hogyan működik a két algoritmus ennek a problémának a megoldásában. Melyik, mikor hatékonyabb, mely esetekben adnak ugyanazon, illetve különböző megoldásokat.

A rend kedvéért az utazó ügynök problémája abban áll, hogy adott N város. Egy ügynöknek körbe kell járnia a városokat úgy, hogy minden várost pontosan egyszer keres fel, és a kiindulási városba kell visszatérnie (gráfelméletben ez a Hamilton kör). A városok közötti utak súlyozottak (legegyszerűbben ez a köztük lévő fizikai távolság, melyet én is alkalmazni fogok), és e súlyok figyelembevételével a legkisebb súlyú (itt legrövidebb) körutat kell megkeresnünk.

Nézzük a két alkalmazott algoritmust. Az ütközésmentesítő algoritmusban egyetlen egyedet használunk. Látszólag ez a lehetőségek beszűkítésének tűnik, de mind lépésszámban, mind a végrehajtási gyorsaságban ez az algoritmus előnyére válik majd. Egy belső ciklusban néhány elemet megváltoztatunk az egyedben, és ha nem kapunk rosszabb egyedet, akkor a változtatást megtartjuk, különben visszavonjuk. Ha elég sokszor ugyanolyan súlyú utat kapunk, akkor egy néhány elemes perturbációval élünk (olyan változtatással, melynél a fitness értéket nem vizsgáljuk). A külső ciklus, melyben az eddigieket ismétli, a felhasználótól függ, bármikor leállíthatja. Lényegében ennyit tud és használ az ütközésmentesítő algoritmus.

A genetikus algoritmusban megválaszthatjuk, hány egyeddel akarunk dolgozni. Az egyedeket első lépésként előállítjuk (ők alkotják a generációt), meghatározzuk fitness értékeit, és e szerinti növekedő sorrendbe rendezzük őket. Így mindig az első egyed lesz a legjobb tulajdonságú. Az algoritmus alkalmaz:

- keresztezést (a legjobb és egy ettől különböző egyed között),

- mutációt (minden egyedre néhány elemet megváltoztat, és ha nem rosszabb megtartja),

- szelekciót (véletlenül előállít egy egyedet, és ha jobb, mint a generáció legrosszabb egyede, akkor lecseréli azt),

- perturbációt (a ciklusok megadható százalékában ellenőrzés nélküli mutációt),

- rendezést (növekedés szerint),

- és végül, ha jobb lett az első egyed fitness értéke, akkor megjelenítést hajt végre.

A leírtakat a felhasználó beavatkozásáig ismétli. Lehetőség van ugyanazzal a kezdeti feltételekkel újra indítani az algoritmusokat.

Nézzük a program futási képét először a Generál gomb megnyomása után, a keresés előtt:

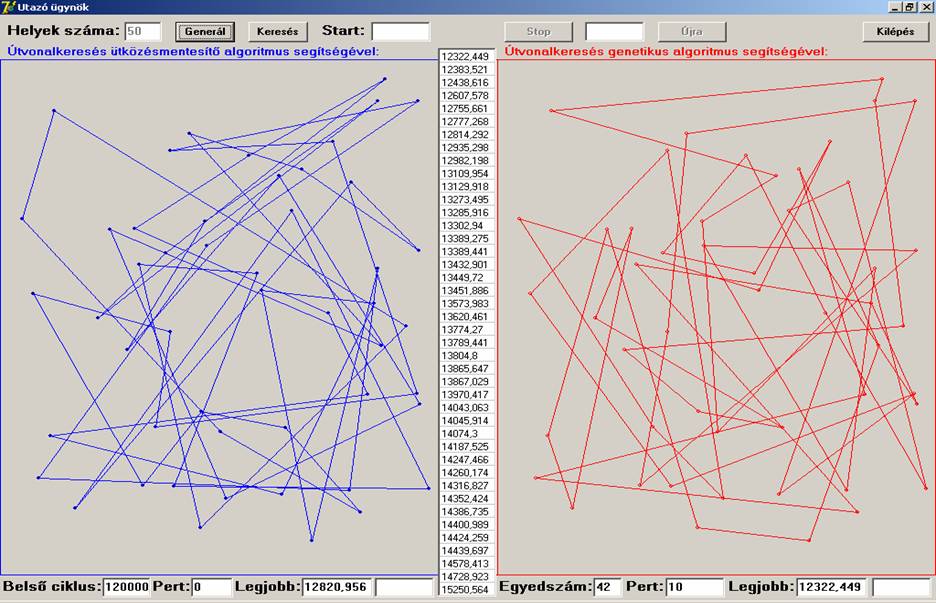
A képernyő bal oldalán az ütközésmentesítő, jobb oldalán a genetikus algoritmus eredménye látható. A helyek száma 50, mely 10 és 500 között választható. A Belső ciklus mérete: 120000. A perturbáció minden 1200-ik lépésben hajtódik végre, azaz 1%-os. A genetikus algoritmus Egyedszáma 42, mely 5 és 42 között választható. Láthatjuk még a Legjobb fitness értékeket külön-külön a két algoritmusra és mellettük az időpontokat, amikor létrejöttek. A keresés a Stop gombbal leállítható, majd ugyanolyan kezdeti feltételekkel, a Keresés gomb megnyomásával újra indítható.

A következő futási képen generálás közben látjuk a program állapotát:

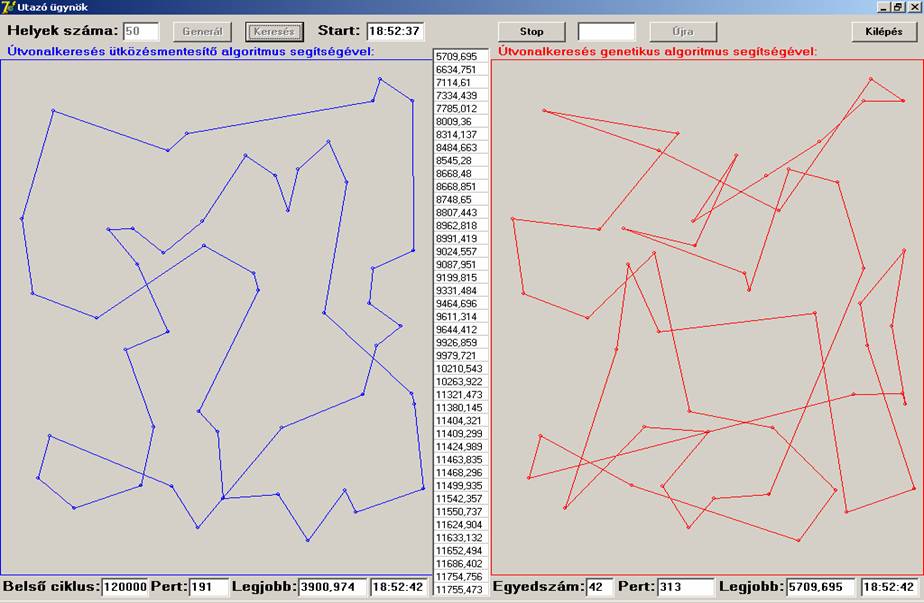
A következő futási képen egy még későbbit:

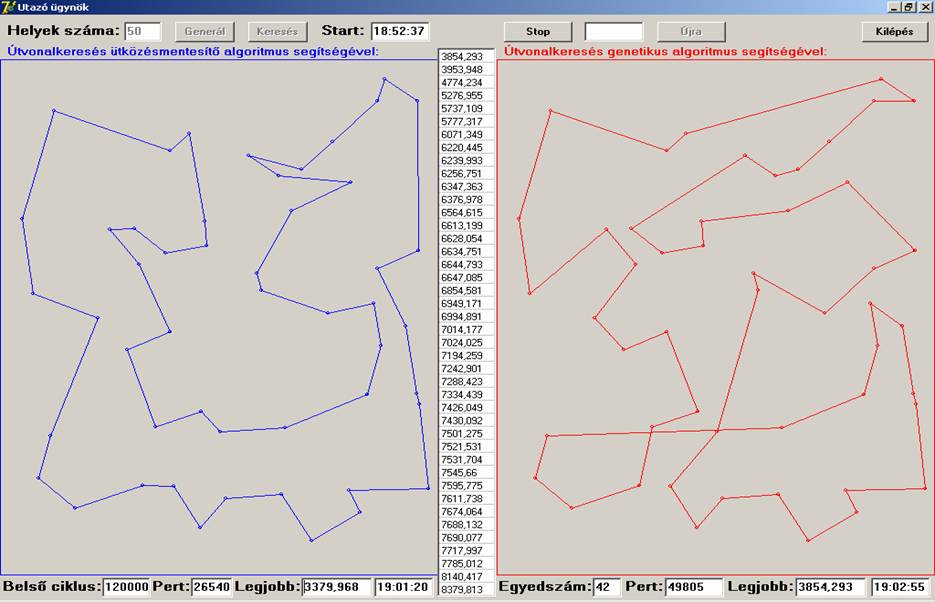
A futási képekből az látszik, hogy az ütközésmentesítő mindkét esetben jobban áll. Most nézzünk olyan eseteket, amikor a Helyek száma kisebb. Rendre: 10, 20, 25, 30, 35 és 40. Futtassuk addig a programot, ameddig még várunk változást. Íme a futtatások eredménye:

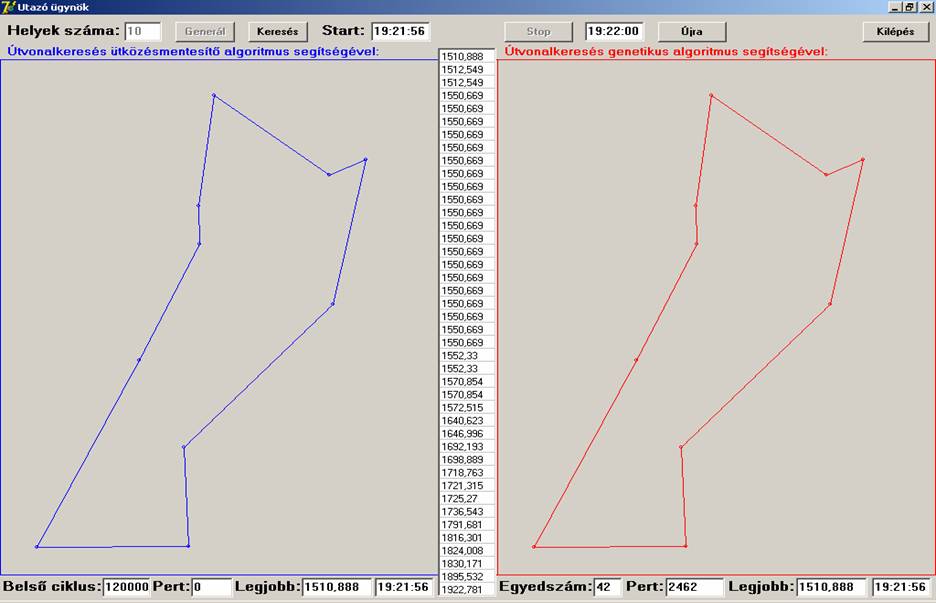
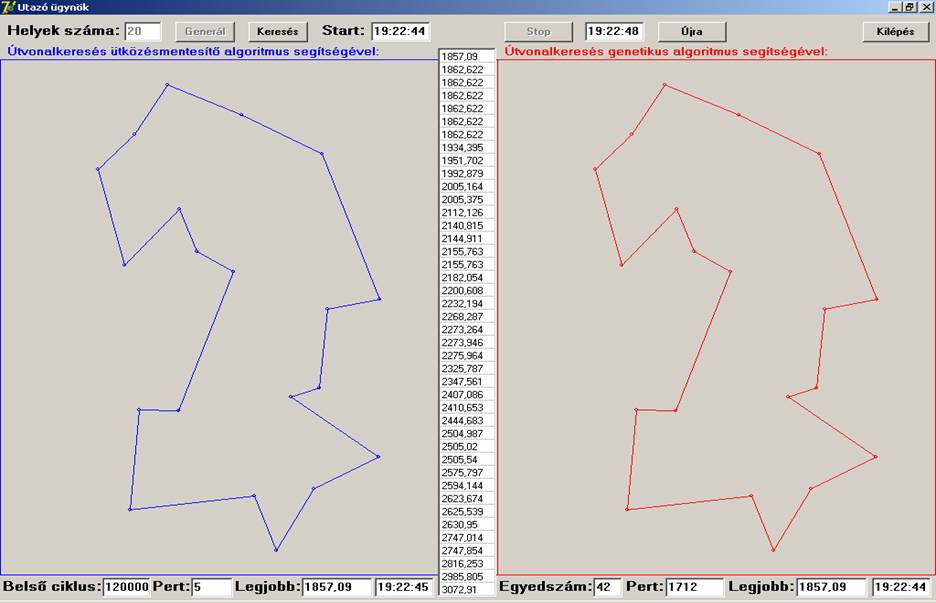
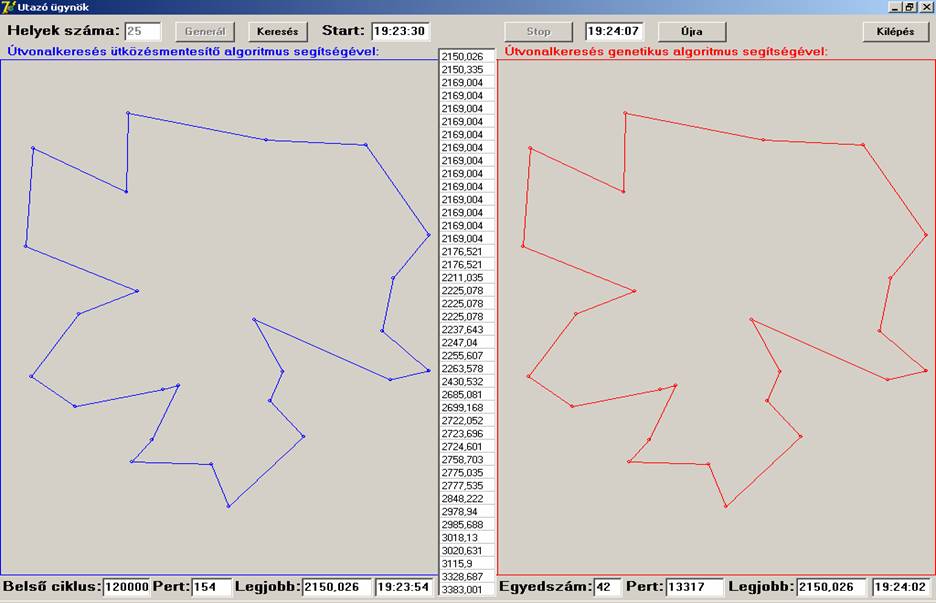
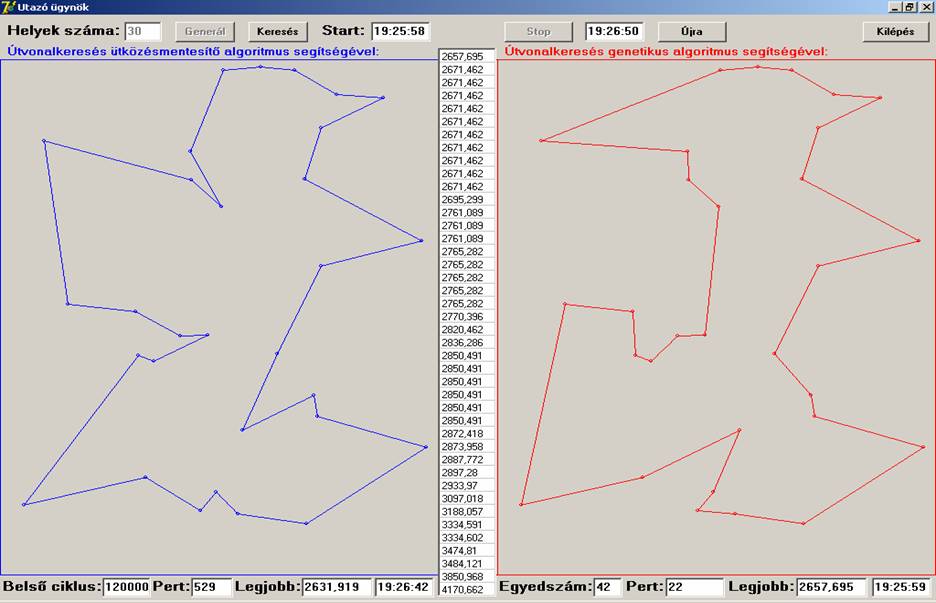
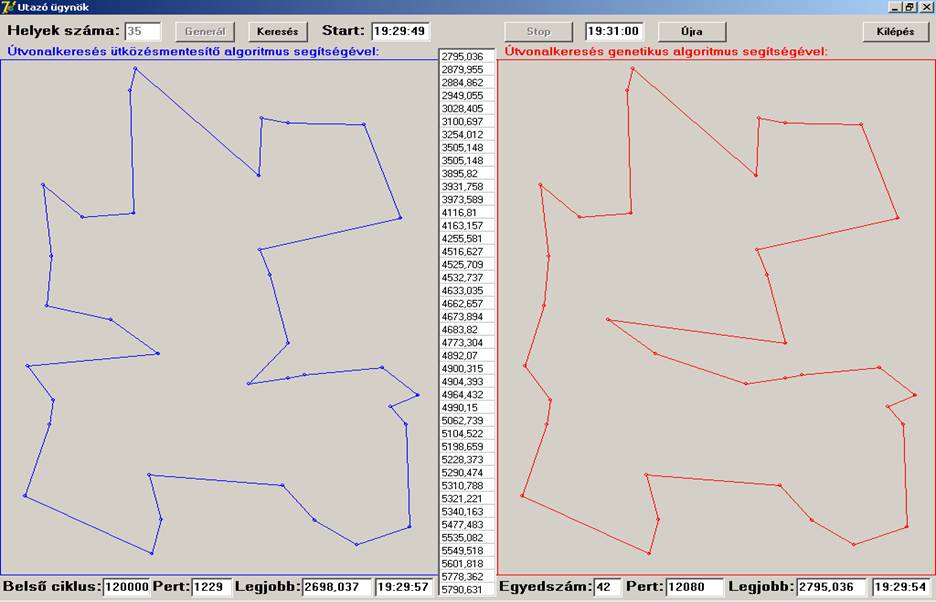
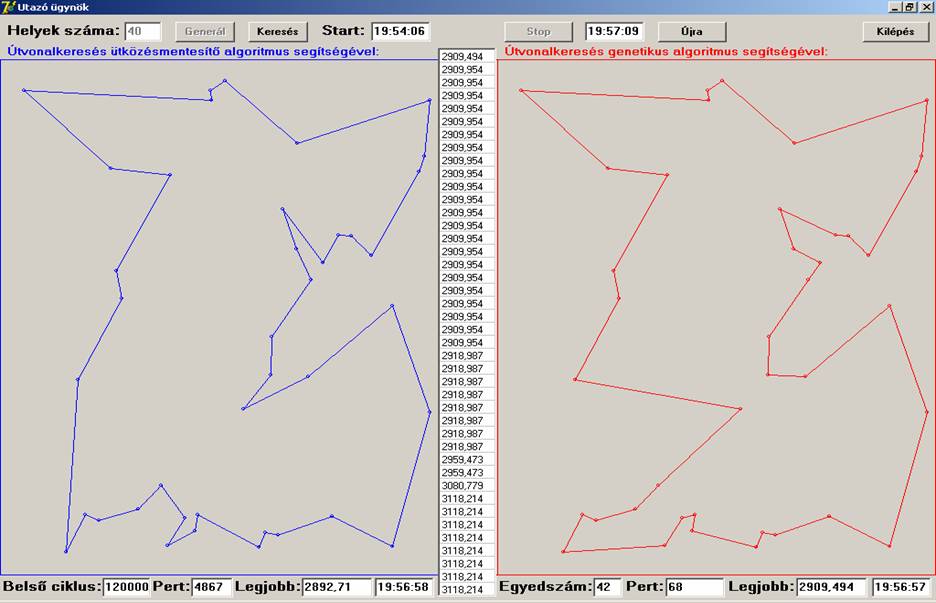
A futtatási eredmények szerint a Helyek száma szerinti 10, 20 és 25 esetekben a két algoritmus ugyanazon eredményeket adta, közel ugyanannyi idő alatt, míg a 30, 35 és 40 esetén az ütközésmentesítő jobban teljesített. Nézzünk egy olyan esetet, amikor a helyek száma 100-as nagyságrendű:

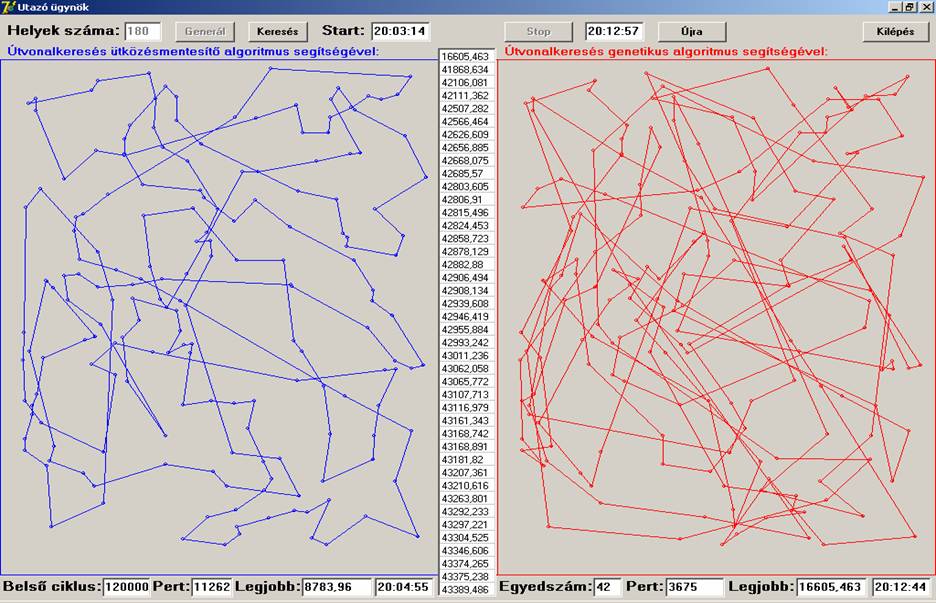
Láthatjuk, hogy az ütközésmentesítő algoritmus sokkal hamarabb, sokkal rövidebb utat talált, mint a genetikus. Ránézve is látható, hogy a genetikus algoritmus által talált körút kusza, sok benne a nagy távolságú összekötés, míg az ütközésmentesítőé strukturáltabb, megtalál sok közeli helyet a keresés során.

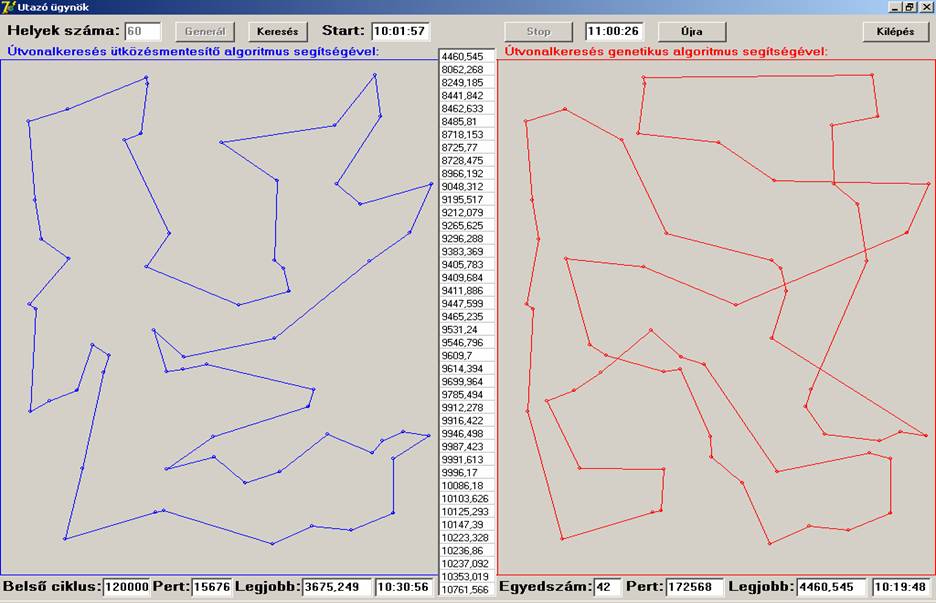
Végül válasszunk egy olyan esetet, amikor a Helyek száma 60 és adjunk kicsit több időt a keresésre. Láthatjuk, hogy az ütközésmentesítő verhetetlennek tűnik: