Barátságos számok

Két természetes számot barátságos szám-párnak nevezünk, ha kölcsönösen igaz rájuk, hogy az egyik szám önmagánál kisebb osztóinak összege egyenlő a másik számmal.

Ilyen például a 220 és a 284 szám-pár, mert 220 önmagánál kisebb osztóinak összege: 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, míg ugyanez 284 esetén: 1 + 2 + 4 + 71 + 142 = 220, vagyis teljesítik a fenti definíciót. A (220; 248) számpárt, mint a legkisebb barátságos számokat, már az ókori görögök is ismerték.

Barátságos számok keresése nagy érdeklődésre tartott számot a történelem folyamán. Igyekeztek minél nagyobb ilyen számokat találni. Míg a középkorban nagy fegyverténynek számított egy-egy újabb számpár felfedezése, a számítógépek megjelenésével a talált szám-párok száma exponenciálisan nőni kezdett. Ma már több mint négymillió barátságos számpárt ismerünk.

A most bemutatandó program elvileg alkalmas arra, hogy a használt programnyelv kereteit figyelembe véve, a lehető legnagyobb értékig az összes barátságos számpárt megkeresse. Nem alkalmaz különleges algoritmust, csak a szokásos osztókeresést és összegzést. Beállíthatjuk a keresési intervallumot, majd start után egy listadobozban jeleníti meg a talált szám-párokat, miközben folyamatosan minden megtalált barátságos számot szöveges állományba ment. Lehetőség van arra is, hogy egy megadható számnál nem nagyobb, egyébként legnagyobb barátságos számpárt megkeressük. Ekkor az első megtalált szám-párnál a keresés befejeződik. Hasonlóképp lehetőség van arra is, hogy egy adott számnál nagyobb, de legkisebb barátságos számpárt megkeressük. A kereséseknél a határ mindig a kisebbik barátságos számra vonatkozik.

A Delphiben az Int64 típussal tárolhatunk legnagyobb egész számot, melynek értéke: 9.223.372.036.854.775.807. Elvileg ilyen nagyságrendű számok között is kereshetnének személyi számítógépeink barátságos számokat, de sajnos már a 16 jegyű számok környékén egyetlen szám osztóinak összegét is csak másodpercek alatt határozzák meg, így értelmes idő alatt nem tudnak megbirkózni a legnagyobb Int64 körüli intervallumban lévő számok vizsgálatával. A programba egyébként ez a lehetőség is be van építve. Tehát ha akár a gépek, akár az algoritmusok javulnak, értelmes lehet ilyen magasságokban is keresgetni a programmal.

Az algoritmus olyan, hogy az intervallumhatár csak a kisebbik számra érvényes, így ha a teljes keresést több intervallum beírásával hajtjuk végre, akkor se marad ki egyetlen barátságos szám sem. A program futási idejének csökkentése érdekében, a képernyőn csak minden tízezredik lépés sorszámát írjuk ki.

A programot a következő paraméterekkel futtattam: Kezdőérték = 1, Végérték = 100 millió. A gép egy 2GHz-es kétmagos Pentium, a futási idő 600 perc körüli volt, és ebben az intervallumban 237 számpárt talált. Kíváncsi voltam a 100 milliót követő első szám-párra, így a következő screen-shot-on még ezt is láthatjuk:

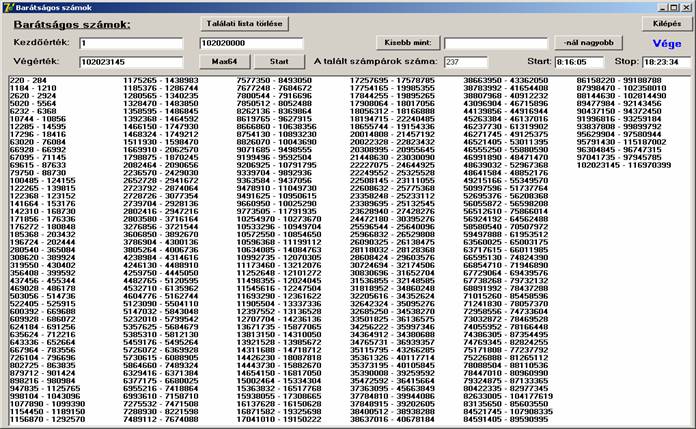
A program listája:

unit UBaratSzam;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls, Grids;

type
TfmBaratSzam = class(TForm)
lbBaratSzam: TLabel;
lbKezdo: TLabel;
edKezdo: TEdit;
lbVegertek: TLabel;
edVegertek: TEdit;
btKilepes: TButton;
btStart: TButton;
ldTalalt: TListBox;
lbVege: TLabel;
btTorles: TButton;
lbSzampSzam: TLabel;
edSzampSzam: TEdit;
ldSzamok: TListBox;
lbStart: TLabel;
lbStop: TLabel;
edStart: TEdit;
edStop: TEdit;
    btMax64: TButton;
edSzam: TEdit;
edMax: TEdit;
btKisebb: TButton;
btNagyobb: TButton;
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure btStartClick(Sender: TObject);
procedure edKezdoChange(Sender: TObject);
procedure edVegertekChange(Sender: TObject);
procedure btTorlesClick(Sender: TObject);
procedure btMax64Click(Sender: TObject);
procedure btKisebbClick(Sender: TObject);
procedure btNagyobbClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

var
fmBaratSzam: TfmBaratSzam;
  Kezd, Vege, Max64: Int64;
DNev: String;
FText: Text;

implementation

{$R *.dfm}

procedure TfmBaratSzam.btKilepesClick(Sender: TObject);
begin
Close;
end;

Function Hatvany(P: Word): Int64;
Begin
If P=0 Then Hatvany:= 1 Else Hatvany:= 2*Hatvany(P-1);
End;

procedure TfmBaratSzam.FormCreate(Sender: TObject);
begin
  Kezd:= StrToInt(edKezdo.Text);
Vege:= StrToInt(edVegertek.Text);
lbVege.Visible:= False;
  Max64:= Hatvany(63)-1;
DNev:= 'barat.txt';
end;

procedure TfmBaratSzam.edKezdoChange(Sender: TObject);
Var Kod: Integer;
begin
With edKezdo Do Val(Text,Kezd,Kod);
end;

procedure TfmBaratSzam.edVegertekChange(Sender: TObject);
Var Kod: Integer;
begin
With edVegertek Do Val(Text,Vege,Kod);
end;

procedure TfmBaratSzam.btMax64Click(Sender: TObject);
begin
edVegertek.Text:= IntToStr(Max64);
end;

procedure TfmBaratSzam.btTorlesClick(Sender: TObject);
begin
ldTalalt.Clear;
ldSzamok.Clear;
edSzampSzam.Text:= '';
edStart.Text:= '';
edStop.Text:= '';
Repaint;
end;

procedure TfmBaratSzam.btStartClick(Sender: TObject);
Var I, J, S1, S2: Int64;
    V: Comp;
Ws: String;
begin
edStart.Text:= TimeToStr(GetTime);
edStop.Text:= '';
lbVege.Visible:= False; Repaint;
  I:= Kezd;
While I<=Vege Do
Begin
If I Mod 10000=0 Then With edSzam Do Begin Text:= IntToStr(I); RePaint End;
If ldSzamok.Items.IndexOf(IntToStr(I))=-1 Then
Begin
      S1:= 1; J:= 2; V:= I;
While J<Sqrt(V) Do
Begin If I Mod J=0 Then Inc(S1,J+(I Div J)); Inc(J) End;
If (J=Sqrt(V)) And (I Mod J=0) Then S1:= S1+J;
If S1>I Then
Begin
        S2:= 1; J:= 2; V:= S1;
While J<Sqrt(V) Do
Begin If S1 Mod J=0 Then Inc(S2,J+(S1 Div J)); Inc(J) End;
If (J=Sqrt(V)) And (S1 Mod J=0) Then S2:= S2+J;
If I=S2 Then
Begin
With ldSzamok.Items Do Begin Add(IntToStr(I)); Add(IntToStr(S1)) End;
With ldTalalt Do
Begin Items.Add(IntToStr(I)+' - '+IntToStr(S1)); RePaint End;
AssignFile(FText,DNev); Append(FText);
WriteLn(FText,I,' - ',S1);
CloseFile(FText);
End;
End;
End;
    Inc(I);
End;
lbVege.Visible:= True;
ldTalalt.Clear;
AssignFile(FText,DNev); Reset(FText);
While Not (EOF(FText)) Do
Begin
ReadLn(FText,Ws);
ldTalalt.Items.Add(Ws);
End;
CloseFile(FText);

edSzampSzam.Text:= IntToStr(ldTalalt.Items.Count);
edStop.Text:= TimeToStr(GetTime);
end;

procedure TfmBaratSzam.btKisebbClick(Sender: TObject);
Var I, J, S1, S2: Int64;
    V: Comp;
    Van: Boolean;
begin
edStart.Text:= TimeToStr(GetTime);
edStop.Text:= '';
lbVege.Visible:= False; Repaint;
  Van:= False;
  I:= StrToInt(edMax.Text);
While Not Van Do
Begin
If I Mod 10000=0 Then With edSzam Do Begin Text:= IntToStr(I); RePaint End;
If ldSzamok.Items.IndexOf(IntToStr(I))=-1 Then
Begin
      S1:= 1; J:= 2; V:= I;
While J<Sqrt(V) Do
Begin If I Mod J=0 Then Inc(S1,J+(I Div J)); Inc(J) End;
If (J=Sqrt(V)) And (I Mod J=0) Then S1:= S1+J;
If S1>I Then
Begin
        S2:= 1; J:= 2; V:= S1;
While J<Sqrt(V) Do
Begin If S1 Mod J=0 Then Inc(S2,J+(S1 Div J)); Inc(J) End;
If (J=Sqrt(V)) And (S1 Mod J=0) Then S2:= S2+J;
If I=S2 Then
Begin
ldTalalt.Items.Add(IntToStr(I)+' - '+IntToStr(S1));
          Van:= True;
End;
End;
End;
Dec(I);
End;
lbVege.Visible:= True;
edSzampSzam.Text:= IntToStr(ldTalalt.Items.Count);
edStop.Text:= TimeToStr(GetTime);
end;

procedure TfmBaratSzam.btNagyobbClick(Sender: TObject);
Var I, J, S1, S2: Int64;
    V: Comp;
    Van: Boolean;
begin
edStart.Text:= TimeToStr(GetTime);
edStop.Text:= '';
lbVege.Visible:= False; Repaint;
  Van:= False;
  I:= StrToInt(edMax.Text);
While Not Van Do
Begin
If I Mod 10000=0 Then With edSzam Do Begin Text:= IntToStr(I); RePaint End;
If ldSzamok.Items.IndexOf(IntToStr(I))=-1 Then
Begin
      S1:= 1; J:= 2; V:= I;
While J<Sqrt(V) Do
Begin If I Mod J=0 Then Inc(S1,J+(I Div J)); Inc(J) End;
If (J=Sqrt(V)) And (I Mod J=0) Then S1:= S1+J;
If S1>I Then
Begin
        S2:= 1; J:= 2; V:= S1;
While J<Sqrt(V) Do
Begin If S1 Mod J=0 Then Inc(S2,J+(S1 Div J)); Inc(J) End;
If (J=Sqrt(V)) And (S1 Mod J=0) Then S2:= S2+J;
If I=S2 Then
Begin
ldTalalt.Items.Add(IntToStr(I)+' - '+IntToStr(S1));
AssignFile(FText,DNev); Append(FText);
WriteLn(FText,I,' - ',S1);
CloseFile(FText);
          Van:= True;
End;
End;
End;
    Inc(I);
End;
lbVege.Visible:= True;
edSzampSzam.Text:= IntToStr(ldTalalt.Items.Count);
edStop.Text:= TimeToStr(GetTime);
end;

end.