Mersenne prímek

A számítógépes információtovábbítás biztonságossá tétele érdekében az adatok titkosítására van szükség. A legelterjedtebb titkosítási mód az RSA, mely egy nyílt kódú, aszimmetrikus titkosító eljárás. Ehhez az eljáráshoz szükség van két elég nagy prímszámra. Ezek szorzata és egy ehhez a szorzathoz relatív prímszám a nyilvános kulcs, melyet mindenki ismerhet. Az egyik prímszámot az információ-küldő, a másikat a fogadó birtokolja. Hatványozás és maradékképzések segítségével a titkosított üzenetet csak a fogadó képes a saját kulcsa segítségével visszafejteni. Az egész eljárás biztonsága attól függ, hogy nyilvános kulcsban szereplő elég nagy prímszámok valóban elég nagyok-e. A cél minél nagyobb prímszámok előállítása, mert minél nagyobb egy szám, prímszám volta, illetve ha nem prím, akkor a szorzattá alakítása, annál hosszabb ideig lehetséges, és itt a hosszú idő alatt évmilliárdokra kell gondolni, még a mai leggyorsabb számítógépekkel is.

Elég nagy prímszám előállításánál leggyakrabban a Mersenne-féle számok között keresnek. A Mersenne-féle számok a következő alakúak:

2^p-1,

ahol a p maga is prímszám. A legnagyobb ismert Mersenne-féle prímszám a 47., mely közel 13 millió tízes számrendszerbeli számjegyként írható fel, és egy mai gyors személyi számítógép egy hónapos munkájának az eredménye.

Az itt található program csak demonstráció, nem képes a fent említett méretű prímszámok közelébe sem érni. Azért az első 10 Mersenne-féle prímet produkálja.

A futtatási kép:

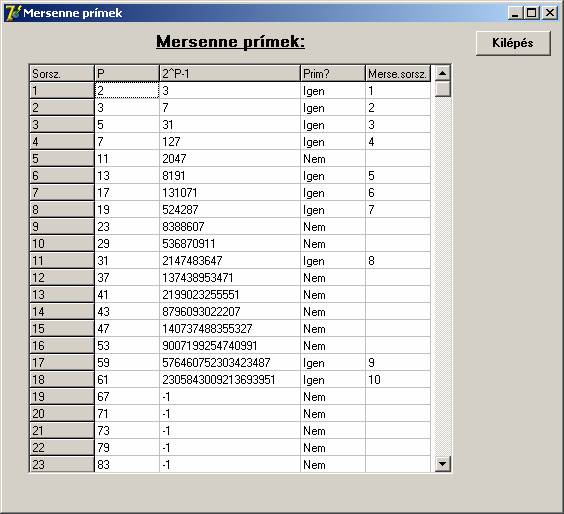
A program listája:

unit UMersenne;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes, Graphics,

Controls, Forms, Dialogs, StdCtrls, Grids;

type
TfmMersenne = class(TForm)
lbMersenne: TLabel;
sgTabla: TStringGrid;
btKilepes: TButton;
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

var
fmMersenne: TfmMersenne;

implementation

{$R *.dfm}

procedure TfmMersenne.btKilepesClick(Sender: TObject);
begin
Close;
end;

Function Prime(S: Int64): Boolean;
Var J: Word;
Begin
Prime:= False; If S In [0,1] Then Exit;
Prime:= True; If S In [2,3] Then Exit;
Prime:= False; If (S Mod 6<>1) And (S Mod 6<>5) Then Exit;
Prime:= True;
For J:= 2 To S-1 Do If (S Mod J)=0 Then
Begin Prime:= False; Break End;
End;

Function Hatvany(P: Word): Int64;
Begin
If P=0 Then Hatvany:= 1 Else Hatvany:= 2*Hatvany(P-1);
End;

procedure TfmMersenne.FormCreate(Sender: TObject);
Var I, N, M: LongInt;
begin
With sgTabla Do
Begin
ColWidths[2]:= 140;

Cells[0,0]:= 'Sorsz.';
Cells[1,0]:= 'P';
Cells[2,0]:= '2^P-1';
Cells[3,0]:= 'Prim?';
Cells[4,0]:= 'Merse.sorsz.';
    I:= 0; M:= 0;
For N:= 1 To 1000 Do If Prime(N) Then
Begin
If RowCount<I+2 Then RowCount:= RowCount+1;
      Inc(I);
Cells[0,I]:= IntToStr(I);
Cells[1,I]:= IntToStr(N);
Cells[2,I]:= IntToStr(Hatvany(N)-1);
If Prime(Hatvany(N)-1) Then
Begin
Cells[3,I]:= 'Igen'; Inc(M); Cells[4,I]:= IntToStr(M);
End
Else Cells[3,I]:= 'Nem';
End;
End;
end;

end.