Pitagoraszi számhármasok

Ha egy derékszögű háromszög oldalainak mérőszáma egész, akkor ezt a három mérőszámot Pitagoraszi számhármasnak nevezzük. A legkisebb és talán legismertebb ilyen három szám: 3,4 és 5. (3² + 4² = 5²). Valamint a kőművesek által, a házak alapjainak derékszögű kijelölésére régóta használt: 60, 80 és 100 (cm), mely az előző számsor 20-sorosa (azaz mint két háromszög egymáshoz hasonló).

Az itt látható programmal tetszőleges létező (a számítógép illetve a használt programnyelv lehetőségei szerinti) Pitagoraszi számhármas meghatározható (kihagyás és hasonlóság miatti ismétlés nélkül). A képzési szabály:

A = M² - N²

B = 2*M*N

C = M² + N²

ahol M>N, az M és N közül az egyik páros a másik páratlan, valamint M és N relatív prímek.

A program az eredményeket egy StringGridben helyezi el, mely sorainak számát dinamikusan növeli. A próbafuttatás M=100-ig történt, és 2040 számhármast állított elő.

A futtatás eredménye:

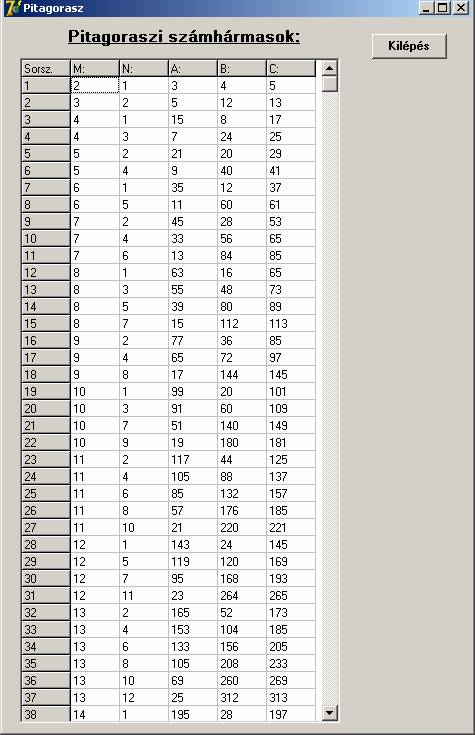
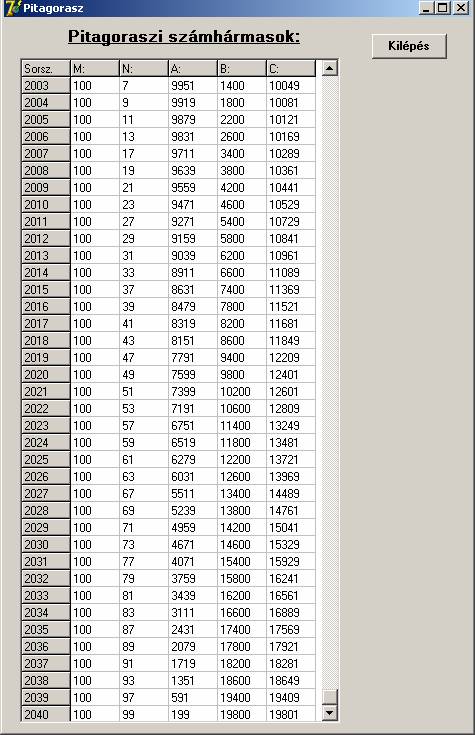
A program listája:

unit UPitagorasz;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes, Graphics, 

Controls, Forms, Dialogs, Grids, StdCtrls;

type
TfmPitagorasz = class(TForm)
lbPitagorasz: TLabel;
sgTabla: TStringGrid;
btKilepes: TButton;
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

var
fmPitagorasz: TfmPitagorasz;

implementation

{$R *.dfm}

procedure TfmPitagorasz.btKilepesClick(Sender: TObject);
begin
Close;
end;

Function RelPrim(P,Q: LongInt): Boolean;
Var R: LongInt;
Begin
Repeat
    R:= P Mod Q;
    P:= Q;
    Q:= R;
Until R=0;
RelPrim:= P=1;
End;

procedure TfmPitagorasz.FormCreate(Sender: TObject);
Var I, J, S: LongInt;
begin
With sgTabla Do
Begin
Cells[0,0]:= 'Sorsz.';
Cells[1,0]:= 'M:';
Cells[2,0]:= 'N:';
Cells[3,0]:= 'A:';
Cells[4,0]:= 'B:';
Cells[5,0]:= 'C:';
    S:= 0;
For I:= 2 To 100 Do For J:= 1 To I-1 Do
If RelPrim(I,J) And (Odd(I) XOr Odd(J)) Then
Begin
If RowCount<S Then RowCount:= RowCount+1;
      Inc(S); Cells[0,S]:= IntToStr(S);
Cells[1,S]:= IntToStr(I);
Cells[2,S]:= IntToStr(J);
Cells[3,S]:= IntToStr(Sqr(I)-Sqr(J));
Cells[4,S]:= IntToStr(2*I*J);
Cells[5,S]:= IntToStr(Sqr(I)+Sqr(J));
End;
End;
end;

end.