Tökéletes számok

Azokat a természetes számokat, amelyek osztóinak összege egyenlő a számmal, tökéletes számoknak nevezzük (az osztók közé bevesszük az 1-et, de magát a számot nem).

Euklidesz felismerte, hogy az első 4 tökéletes szám alakja:

2^(n-1)*(2ⁿ-1),

sőt azt is bebizonyította, ha 2ⁿ-1 prím, akkor a képlet tökéletes számot határoz meg. A 2ⁿ-1 alakú prímszámokat Mersenne prímeknek nevezzük. Eddig még csak páros tökéletes számokat ismerünk. Nem ismert, hogy létezhet-e egyáltalán páratlan tökéletes szám. Az is bizonyításra vár, hogy a tökéletes számok száma véges-e vagy végtelen. Euler bebizonyította, hogy Euklidesz képlete az összes páros tökéletes számot megadja. Viszont a Mersenne prímek számosságát sem ismerjük, így ez sem segít a tökéletes számok számosságának megítélésében.

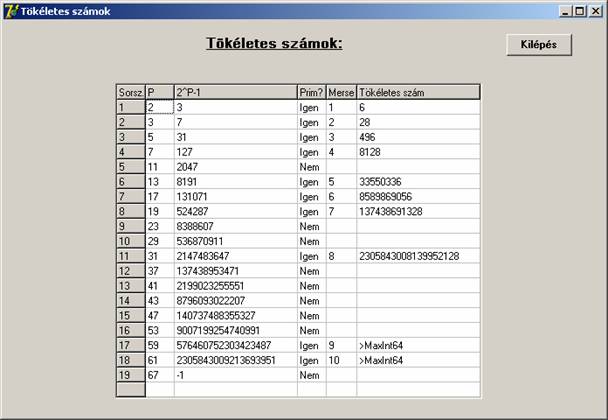
Ez a program az első 10 Mersenne prím mellett az első 8 tökéletes számot is szolgáltatja, a 9. és 10.-re már túlcsordul.

A futási kép:

A program listája:

unit UTokeletes;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls, Grids;

type
  TForm1 = class(TForm)
lbTokeletes: TLabel;
sgTabla: TStringGrid;
btKilepes: TButton;
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

procedure TForm1.btKilepesClick(Sender: TObject);
begin
Close;
end;

Function Prime(S: Int64): Boolean;
Var J: Word;
Begin
Prime:= False; If S In [0,1] Then Exit;
Prime:= True; If S In [2,3] Then Exit;
Prime:= False; If (S Mod 6<>1) And (S Mod 6<>5) Then Exit;
Prime:= True;
For J:= 2 To S-1 Do If (S Mod J)=0 Then
Begin Prime:= False; Break End;
End;

Function Hatvany(P: Word): Int64;
Begin
If P=0 Then Hatvany:= 1 Else Hatvany:= 2*Hatvany(P-1);
End;

procedure TForm1.FormCreate(Sender: TObject);
Var I, N, M: LongInt;
begin
With sgTabla Do
Begin
ColWidths[0]:= 32;
ColWidths[1]:= 32;
ColWidths[2]:= 140;
ColWidths[3]:= 32;
ColWidths[4]:= 34;
ColWidths[5]:= 140;

Cells[0,0]:= 'Sorsz.';
Cells[1,0]:= 'P';
Cells[2,0]:= '2^P-1';
Cells[3,0]:= 'Prim?';
Cells[4,0]:= 'Merse';
Cells[5,0]:= 'Tökéletes szám';
    I:= 0; M:= 0;
For N:= 1 To 70 Do If Prime(N) Then
Begin
If RowCount<I+2 Then RowCount:= RowCount+1;
      Inc(I);
Cells[0,I]:= IntToStr(I);
Cells[1,I]:= IntToStr(N);
Cells[2,I]:= IntToStr(Hatvany(N)-1);
If Prime(Hatvany(N)-1) Then
Begin
Cells[3,I]:= 'Igen'; Inc(M); Cells[4,I]:= IntToStr(M);
If Hatvany(N-1)*(Hatvany(N)-1)>0 Then
Cells[5,I]:= IntToStr(Hatvany(N-1)*(Hatvany(N)-1)) Else
Cells[5,I]:= '>MaxInt64';
End
Else Cells[3,I]:= 'Nem';
End;
End;
end;

end.