Alaptáblák

Ha olyan programot akarunk készíteni, amely alkalmas Sudoku feladványok készítésére, akkor annak tudnia kell alaptáblát előállítani, feladványt megoldani, és ha minősíteni is szeretnénk a feladványainkat, akkor természetesen azt is. Az elkészült alaptáblákat és feladványokat célszerű valamilyen lemezes állományban tárolni a későbbi felhasználhatóság érdekében. Én a könnyebb kezelhetőséget szem előtt tartva, tipizált állományban tárolom a feladványokat.

Nézzük a szükséges deklarációkat:

Const

GAl=3;                       {generalasi alapszam (3)}
Max=GAl*Gal;                 {a kis negyzet vagy tartomany (9)}
  MX=Max*Max;                  {a teljes tabla (81)}


Type

  St81=String[81];             {a tabla es a megoldas stringje}
KTomb=Array[1..Max] Of Word; {kis tomb (9)}
TTomb=Array[1..MX] Of Word;  {nagy tomb (81)}

  TGT=Record
TTabla: St81;              {az alaptabla rekordja}
End;

  TGS=Record {feladvany rekord}
    Ind: LongInt;              {tombindex}
Tabla, Megold: ST81;       {a feladvany es a megoldas tombje}
    Elem, NFok: Word;          {a feladvany elemszama es nehezsegi foka}
End;

Var

DNev: String;                {operacios rendszerbeli file nev}
GTFile: File Of TGT;         {az alaptabla allomany logikai neve}
GSFile: File Of TGS;         {a feladvany allomany logikai neve}
ATbl: TGT;                   {egy teljes tabla}
ARek: TGS;                   {aktualis rekord a file olvasasanal}
  ST: TTomb;                   {az alaptabla kiindulasi tombje}
  SA: TTomb;                   {alaptabla tombje egy feladvanynal}
  SM: TTomb;                   {feladvany tombje}

TIndex: Array[1..Max,1..Max] Of Word; {rogzitett tablaindexek}
InX, InY, InT: TTomb;        {rogzitett oszlop-, sor- es tartomanyindexek}
TKInd: TTomb;                {rogzitett tartomanyi kezdoindexek}
UtTbl: Array[1..MX,1..MX] Or Word; {ahol ket cella szobatars, ott erteke 1}
SzT: Array[1..MX,1..20] Of Word; {a szobatarsak indexenek tombje}

Következzék egy kis magyarázat. A generálási alapszám megadásával egyszerűen meg lehet változtatni az alaptábla méretét. Ha például 2-t választunk, akkor 4 x 4-es feladványokat, ha 4-et, akkor pedig 16 x 16-os feladványokat készíthetünk a programmal.

A lemezes állományban a táblákat 81-es méretű stringben tárolom, míg a feldolgozás, generálás 81-es méretű számtömbökben történik. A lemezműveleteknél, amely aránylag ritkán fordul elő (főleg ha alacsony elemszámú feladványt készítünk) átváltást kell végrehajtani a két típus között.

Az alaptáblákban az elemek tartomány-sorfolytonosan vannak elrendezve, azaz először a bal felső tartomány kilenc eleme sorfolytonosan, majd középső felső tartományé, aztán a jobb felső tartományé, stb. Végül a jobb alsó tartomány elemeit helyezzük be. Ez a sorrend jelenti a 81-es egydimenziós tömbbeli helyüket. Az alaptábla generálásánál csak egy tartományon belül cserélgetjük az elemeket, így csak sor- és oszlopütközéseket kell figyelni. Az alaptábla generálás előtti feltöltését (ST tömb) a következő ScreeShot-on láthatjuk:

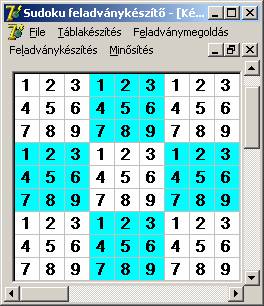
Ez pedig egy kész alaptábla (SA tömb):

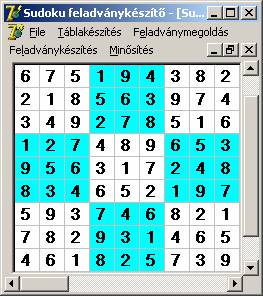
A programban gyakran kellene meghatározni az alaptábla eleminek helyét a lineáris tömbben ezért ezeket a program futtatásának elején kiszámoljuk, és egy TIndex táblázatban rögzítjük. Ennek értékei láthatók a következő ScreenShot-on:

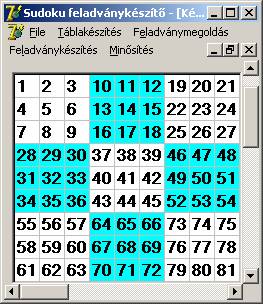
Hasonlóan gyakran kell meghatározni, hogy egy elem milyen indexű sorban, oszlopban vagy tartományban van, ezért ezekre az értékekre hasonlóan járunk el mint a TIndex esetén. Példaként az InT és TKInd tömböket láthatjuk itt:

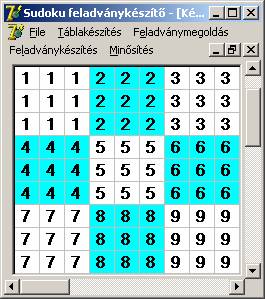
Az InT tömb.

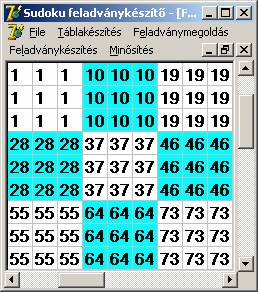
A TKInd tömb.

Kicsit összetettebb az UtTbl és az SzT táblák előállítása. Ezek feltöltésére a következő programsorok alkalmasak:

//utkozesi tabla toltese
For I:= 1 To MX Do For J:= 1 To MX Do UtTbl[I,J]:= 0;
//soronkent
For L:= 0 To GAl-1 Do For KK:= 0 To GAl-1 Do For J:= 1 To Max Do For I:= 1 To Max Do
UtTbl[TIndex[I,L*GAl+(J-1) Div GAl+1],J+K*Max+L*GAl*Max]:= 1;
//oszloponkent
For L:= 0 To GAl-1 Do For K:= 0 To GAl-1 Do For J:= 1 To Max Do For I:= 1 To Max Do
UtTbl[TIndex[(J-1) Mod GAl+1+K*GAl,I],J+K*Max+L*GAl*Max]:= 1;
//tartomanyonkent
For I:= 1 To MX Do
For J:= Max*((I-1) Div Max)+1 To Max*((I-1) Div Max)+Max Do UtTbl[I,J]:= 1;
//atlo torlese
For I:= 1 To MX Do UtTbl[I,I]:= 0;

//szobatarsak
For I:= 1 To MX Do For J:= 1 To 20 Do SzT[I,J]:= 0;
For I:= 1 To MX Do
Begin
  K:= 0; For J:= 1 To MX Do If UtTbl[I,J]=1 Then
Begin Inc(K); SzT[I,K]:= J End;
End;

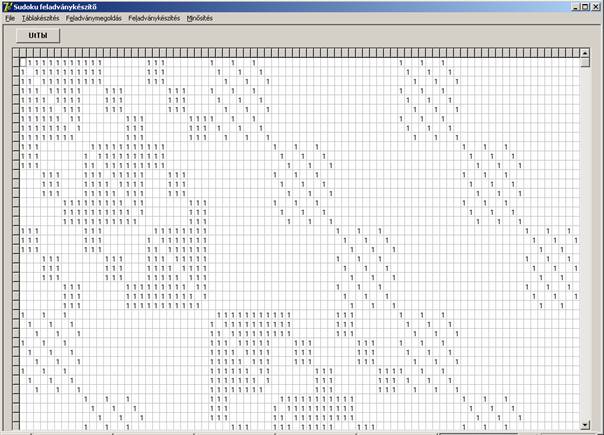
Az ütközési tábla (UtTbl) egy része (az első 41 sora) így néz ki:

Végül lássuk az alaptábla (SA tömb) generálási kódját:

Procedure Csere(A, B: Word);
Var P: Word;
Begin
  P:= SA[A]; SA[A]:= SA[B]; SA[B]:= P;
End;

Function Utkozes: Word;
Var I, J, K, U: Word;
Begin
  U:= 0; For I:= 1 To Max Do For J:= 1 To Max Do For K:= 1 To 20 Do
If SA[TIndex[I,J]]=SA[SzT[TIndex[I,J],K]] Then Inc(U); Utkozes:= U;
End;

Procedure Alap;
Var A, B, I, P, U: Word;
Begin
//start allapot
  SA:= ST;
//kever
For I:= 1 To MX Do
Begin
    A:= Random(MX)+1;
Repeat B:= Max*((A-1) Div Max)+Random(Max)+1 Until A<>B;
    Csere(A,B);
End;
//rendez
  U:= MX*MX;
While U>0 Do
Begin
A:= Random(MX)+1; B:= Max*((A-1) Div Max)+Random(Max)+1;
    P:= U; Csere(A,B); U:= Utkozes;
If U>P Then Begin Csere(A,B); U:= P End;
End;
End;