Feladványkészítés

Az első Sudoku feladványkészítő programomba 2011 tavaszán kezdtem bele. Akkor még nem tudtam, hogy ez mennyire bonyolult, nehezen megoldható problémát jelent számomra. Közben erősen lekötötte programozási időmet a TFOR órarendkészítő program is, melyet 2012 novemberére sikerült befejeznem – vagyis sokkal könnyebb volt, mint a Sudoku feladványkészítés. Ettől kezdve intenzívebben foglalkozhattam a Sudokuval. Az első, magasabb elemszámú (21-39) feladványok már aránylag hamar létrejöttek. De az első 20 elemű feladványt csak 2013 december elején, az első 19-est 2013 december végén, míg az első 17-est 2014 áprilisában sikerült létrehoznom. Ettől kezdve szinte mindig az motivált, hogy minél több, minél kisebb elemszámú (természetesen 17-nél nem kisebb) feladványt generáljak, mert ez jelentette számomra az igazi kihívást. Ez látszik a jelenlegi feladványkészletemen is, amely 4,5 millió feladványt tartalmaz és ebből 1 millió 18-as, 500 ezer pedig 17-es elemszámú – körülbelül.

A gépi feladványkészítésnek két alapvetően különböző módszerét különböztetném meg. Az első esetben az alaptáblából (egy helyesen kitöltött teljes táblából) indul a keresés. Mindig egy újabb elemet törlünk a táblából, megnézzük hogy helyes feladványt kaptunk-e, ha igen akkor újra törlünk és vizsgálunk, ha nem helyes, akkor visszatérünk az előző, még jó feladványhoz, mint eredményhez. A helyes (vagy jó) feladvány itt azt jelenti, hogy a használt metódusokkal megoldható-e. A második esetben egy üres feladványtáblából indulunk. Ahány elemű feladványt szeretnénk készíteni, annyi elemet véletlenül elhelyezünk a táblán, majd addig hajtunk végre változtatásokat az elemeken, ameddig helyes feladványt nem kapunk. Az első készítési típust direkt a másodikat indirekt feladványkészítő módszernek nevezem.

Most nézzük meg egy kicsit jobban a direkt módszert. A generálás közben hamar kiderült, hogy a legtöbb ilyen módszerrel előállítható feladvány 24-25 elemszámú. Ha ennél kisebb elemszámút szeretnénk csak előállítani, akkor ezt korlátozni kell. Ennek az lett az eredménye, hogy a szükségesnél nagyobb elemszámúakat a program eldobta, nem rögzítette. Látszólag a generálási idő megnőtt. Lássuk, hogy néz ez ki a programomban (a látvány szerintem egyértelmű, részletesen nem elemezném a képernyőt):

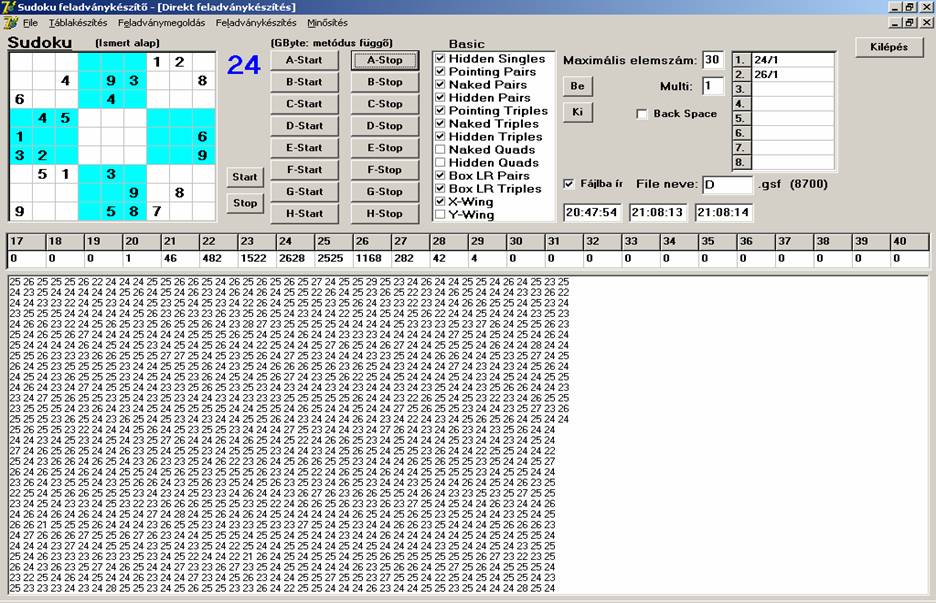
A generálást a program 7486 darab feladványnál kezdte, így 1220 másodperc alatt 1214 darab feladványt állított elő (gyakorlatilag) másodpercenként 1-et. Látható továbbá, hogy ezzel a módszerrel 20 vagy ez alatti elemszám esetén nagyon megnő a generálási idő. Körülbelül 2,4 órát kellene várni arra, hogy 20-as feladvány létrejöjjön. Az előállított feladványok között – a számos alkalmazott algoritmus miatt – magasabb nehézségi fokút is találhatunk. Nézzük mi a helyzet, ha csökkentjük a metódusok számát. Használjunk például csak HS-t:

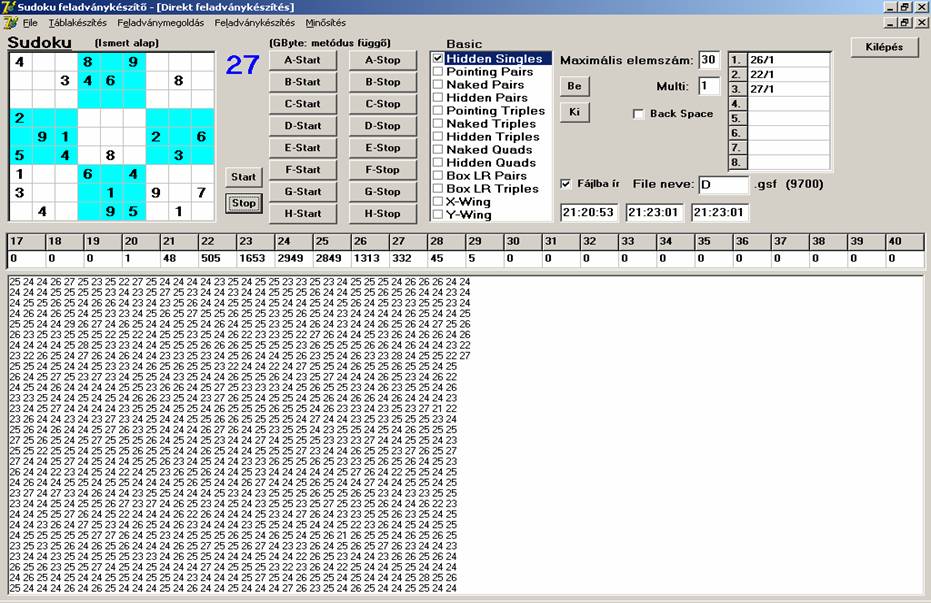
Most az 1000 db elkészítéséhez 128 másodpercre volt szükség, ami 7,8-szeres sebességet jelent az előzőhöz képest. Próbálkozzunk meg csak BS használatával. Ezt kaptuk:

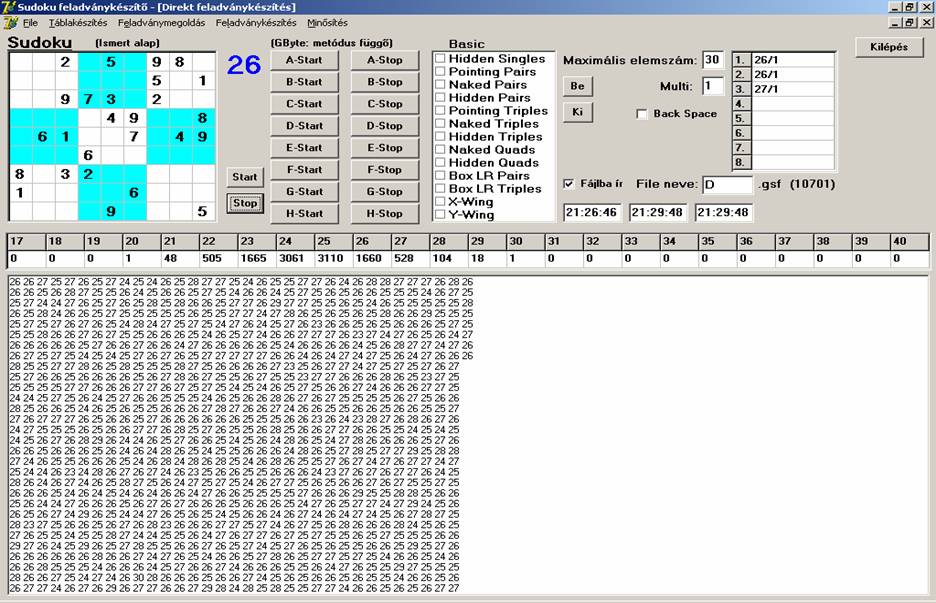
Ekkor a következők figyelhetők meg: a generálási idő növekedett, azaz a HS nagyon hasznos a generálás szempontjából még akkor is, ha több lépést kell végrehajtani egy ciklusban, de a hatékonysága mindezt kompenzálja. A másik, amit észrevehetünk az, hogy az a generált feladványok elemszáma a nagyobb értékek felé eltolódott (például létrejött egy 30-as elemszámú is).

Térjünk át az indirekt módszerre. Állítsuk be úgy a kezdeti feltételeket, hogy a program 18-21 elemű feladványokat keressen (korábban már használtam 40-es elemszámúra, 583 db-ot állítottam vele elő). Most is megfigyelhető, hogy a megengedett lehetőségek közül a nagyobb elemszámúakat gyakrabban tudja előállítani.

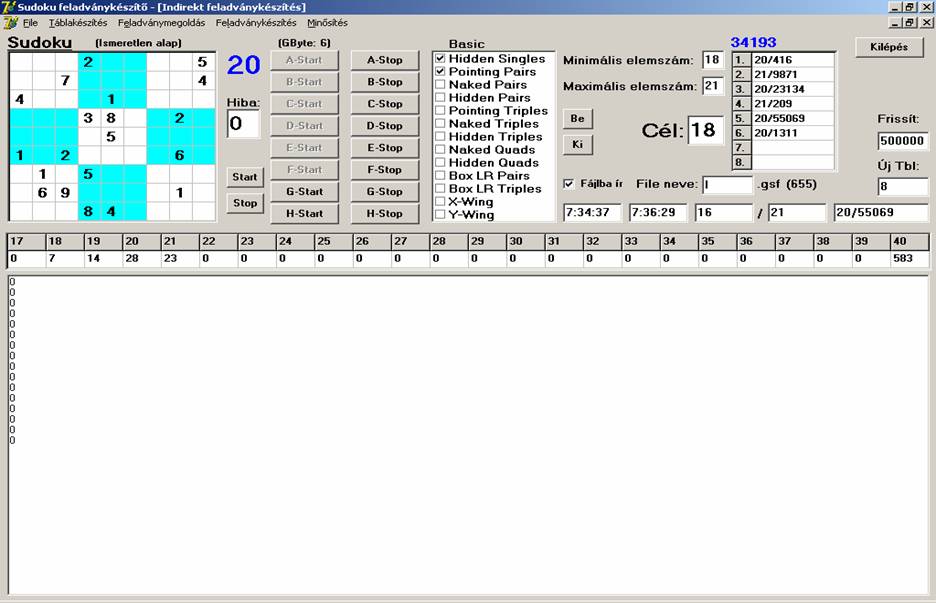
A képernyőről leolvasható, hogy a mostani futtatás alatt egy feladvány átlagosan 34193 ciklus alatt jött létre, 21 generálási próbálkozásból 16 eredményes volt, közben 8-szor kellett teljesen újra kezdeni a generálást (51 feladvány már korábban készült). A teljes 72 előállított feladványból 7db 18-as, 14 db 19-es, 28 db 20-as és 23 db 21-es. A generálási idő viszont még mindig elég nagy (21 db/112 sec). Ilyen tempóban milliós nagyságrendű feladványt előállítani képtelenség. Tehát még van mit javítani az algoritmuson, újabb ötletek szükségesek.

A direkt és indirekt módszert összehasonlítva úgy tűnik, hogy a direkt gyorsabb, viszont az indirekt módszerrel lehet egyáltalán alacsony elemszámú feladványokat generálni. Mindkét módszer még önmagában javítható. Az eljárások viselkedéséért az algoritmusok magjában található ütközésmentesítő eljárás a felelős. Mint genetikus algoritmus az aktuális egyed, magában hordozza azt a tulajdonságát – mely számunkra eléggé rejtve marad – amivel a megoldás felé sodródik az egyed. Ezt az átalakulást – úgy látszik – az ismert alaphoz való ragaszkodás gátolja. Igaz, hogy a direkt módszernél az egyed minden állapotban egy helyesen kitöltött tábla része, csak a kiválasztási lehetőség is olyan nagy, hogy ebből a jó út nehezen található. Amikor ez a kötöttség nincs, akkor a köztes egyedek nem feltétlen egy helyes tábla részei. Viszont nemcsak a jó, hanem a rossz egyedekből is tud részmegoldásokat meríteni, (a hibákból is tanul) és így a kisebb elemszámú feladványoknál is eredményes (eredményesebb) tud lenni.