A metódusok vizsgálata

A feladványok megoldása lapokon többek között a jelöltek számának csökkentésére alkalmas metódusokat, eljárásokat ismerhettük meg. Megadtam egy-egy lehetséges implementációját is. A metódusokat most olyan szempontból vizsgálom meg, hogy egy adatbázis feladványain milyen sebességgel és milyen eredményességgel alkalmazhatók. Azért, hogy a metódusok leírását ne kelljen az előző lapokról megnézni, most itt megismétlem:

Hidden Singles (HS): Ha egy sorban, egy oszlopban vagy egy tartományban csak egyetlen cellában van egy adott jelölt, akkor a cellába ez a jelölt beírható, és a szoba további celláiból a jelölt törölhető.

Pointing Pairs (PP): Ha egy tartományban egy jelölt csak két helyen van, de egy sorban vagy egy oszlopban, akkor a jelölt – a kijelölt teljes sorban vagy oszlopban – a többi helyről törölhető.

Naked Pairs (NP): Ha egy szobának két cellájában csak ugyanaz a két jelölt van, akkor a szoba többi cellájából (a kijelölt sorból vagy oszlopból, és ha egy tartományban vannak, akkor tartományból is) ezek a jelöltek törölhetők.

Hidden Pairs (HP): Ha egy szobában csak két cellában van ugyanaz a két jelölt (de más még lehet), akkor a szoba ezen két mezőjéből minden más jelölt törölhető.

Pointing Triples (PT): Ha egy tartományban egy jelölt csak három helyen van, de egy sorban vagy egy oszlopban, akkor a kijelölt sorban vagy oszlopban a többi helyről a jelölt törölhető.

Naked Triples (NT): Ha egy szobában, három cellában (egy sorban, egy oszlopban vagy egy tartományban) van csak ugyanaz a három jelölt, akkor a többi cellából ezek a jelöltek törölhetők.

Hidden Triples (HT): Ha egy szobában csak három cellában (egy sorban, egy oszlopban vagy egy tartományban) található három jelölt (de más még lehet), akkor a szoba ezen három mezőjéből minden más jelölt törölhető.

Naked Quads (NQ): Ha egy szobában van olyan négy nem üres cella (egy sorban, egy oszlopban vagy egy tartományban), amelyben összesen négy jelölt van, akkor a többi helyről ezek a jelöltek törölhetők.

Hidden Quads (HQ): Ha egy szobában csak négy cellában (értelemszerűen egy sorban, egy oszlopban vagy egy tartományban) található négy jelölt (de más jelölt még lehet), akkor ezen négy cellából a többi jelölt törölhető.

Box Line Reduction Pairs (BP): Ha egy oszlopban vagy sorban egy szám kétszer egy tartományon belül ismétlődik, és csak kétszer szerepel az oszlopban vagy sorban, akkor a tartományon belül a többi helyről törölhető.

Box Line Reduction Triples (BT): Ha egy oszlopban vagy sorban egy jelölt háromszor egy tartományon belül ismétlődik, és csak háromszor szerepel az oszlopban vagy sorban, akkor a tartományon belül a többi helyről törölhető.

X-Wing (XW): Ha két jelölt két oszlopban pontosan kétszer-kétszer szerepel, de ugyanabban a két sorban, akkor a két sor további helyeiről a jelölt törölhető.

Y-Wing (YW): Ha három jelölt (legyenek: A, B és C) úgy helyezkedik el egy derékszögű háromszög csúcsainak megfelelő cellákban, hogy mindegyikben pontosan kettő, de bármely két cella jelöltjei között csak egy közös található (azaz: A és B, A és C valamint B és C), akkor a hegyesszögű csúcsok sorának illetve oszlopának metszésében lévő cellából a hegyesszögű csúcsokban lévő cellák közös jelöltje törölhető.

Válasszunk egy olyan adatbázist, amelyben különböző elemszámú és nehézségi fokú feladványok találhatók. Ilyen például a D.gsf (7486):

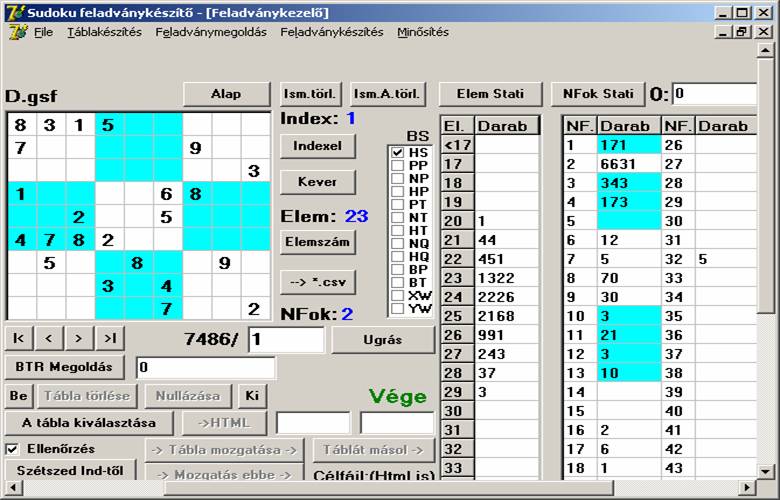
Látható, hogy az elemszámok 20 és 29 között, a nehézségi fokok 1 és 32 között változnak. A kézi megoldót kiegészítettem egy Metódus kontroll funkcióval, mely a kiválasztott metódust alkalmazza az adatbázis összes feladványán, megjegyzi és összeszámolja, hogy hány feladvány esetén volt eredményes és a vizsgálat mennyi ideig tartott. Lássuk ezt a Naked Triples esetére:

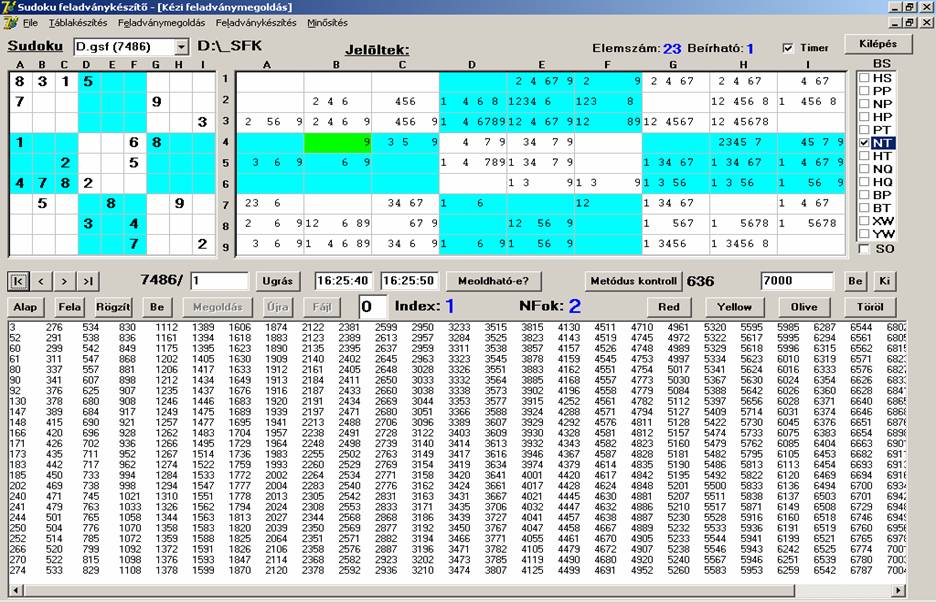
Az eredmény: 636 feladványban volt eredményes (csökkentette a jelöltek számát) és 10 s volt a vizsgálat ideje. Módszeresen végigvizsgáltam az adatbázist az összes metódussal. Az eredményt egy táblázatban rögzítettem:

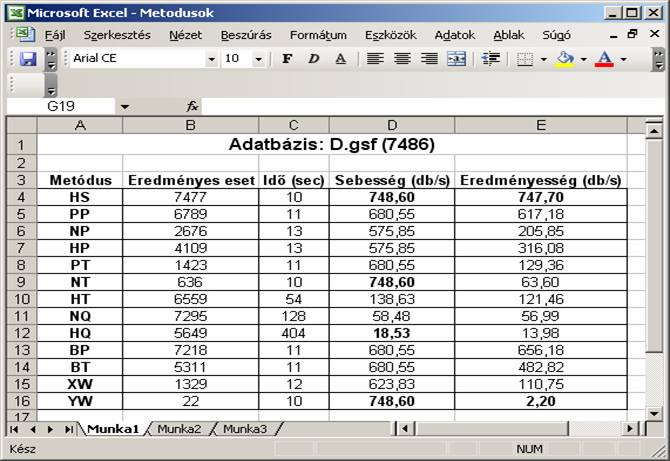
Rövid elemzéssel megállapíthatjuk, hogy három metódus (HS, NT és YW) ugyanolyan, a legnagyobb sebességgel haladt végig az adatbázison. Ugyanakkor a legeredményesebb a HS, és a legeredménytelenebb az YW is ezek között volt. A legkisebb sebességűnek a HQ bizonyult. Eredményesség szempontjából a BP lett a második helyezett és a PP a harmadik. Miért lehetnek érdekesek ezek az eredmények? Egyrészt ha a metódus lassan dolgozott (HQ), akkor meg lehet vizsgálni a kódját, hátha javíthatunk rajta. Másrészt, ha a kódot már nem gondoljuk javíthatónak, akkor a feladványok generálásánál olyan metódusokat célszerű választani, amelyek eredményessége magas, ha a minél rövidebb gépi idő alatt minél több feladvány elérése a cél. Különösen fontos ez az alacsony elemszámú feladványok (például minimum Sudoku) generálásakor.

Nagyon nyilvánvaló, hogy a metódusok között kereszthatás lehetséges, amennyiben egynél több aktív a feladvány elemzésénél. Most ezzel foglalkozzunk egy kicsit. Ehhez a D-20.gsf (3427)-es adatbázist fogjuk használni. Most nem a futási idő, hanem az eredményes esetek száma lesz az érdekes. Mivel 13 metódusból nagyon sokféleképpen lehet néhányat kiválasztani, a teljes elemzéstől most eltekintek (szerintem értelme sem lenne). Néhány páros kiválasztás mellett egy háromszoros kiválasztást is megvizsgálok.

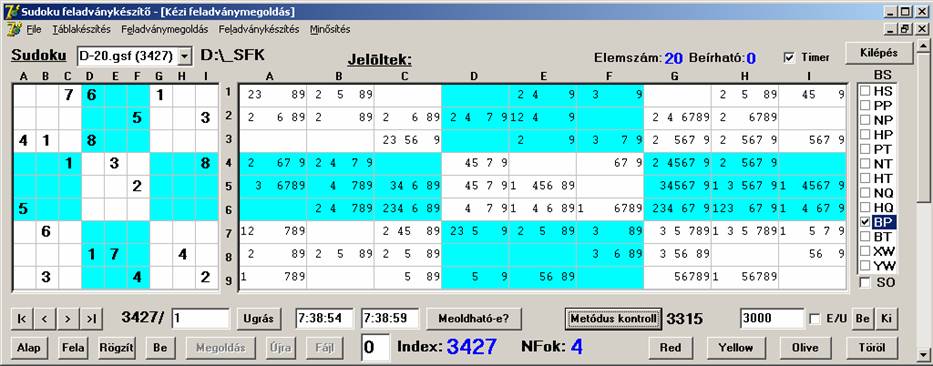
Nézzük meg a két legeredményesebb és leggyorsabb metódus hatását az adatbázison (HS és BP):

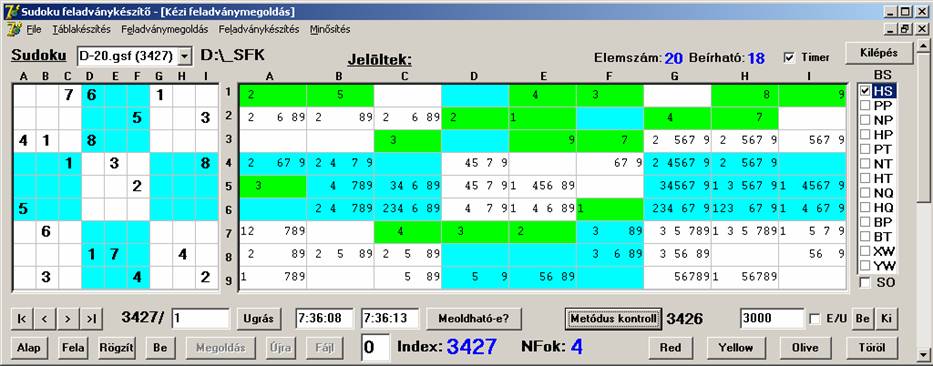
Ez szép, majdnem 100%-os az eredmény.

Ez sem rossz a maga 77%-ával.

Most nézzük meg, mi történik akkor, ha minkét metódus aktív és a BP értékelődik ki másodjára:

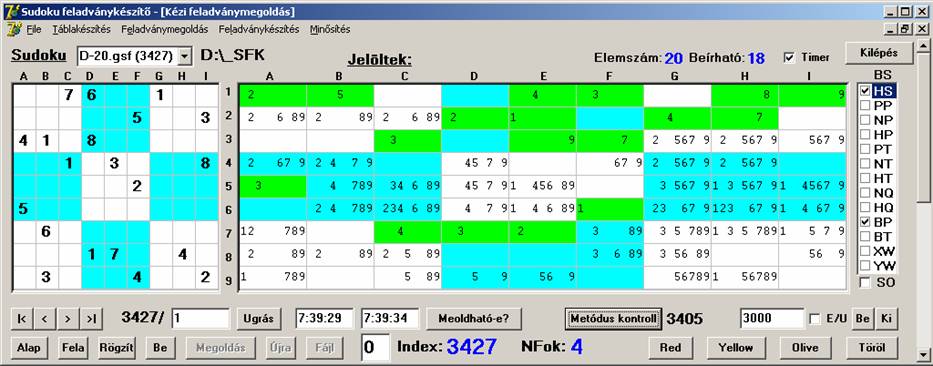
Most pedig fordítva, a HS kiértékelése lesz később:

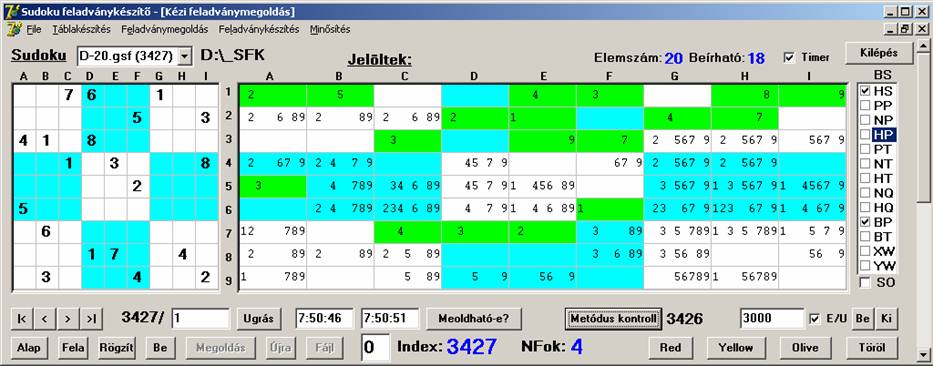
Látható, hogy BP egyedül a legrosszabb a négy eset közül. Ha a HP értékelődik ki később, akkor 21 lehetőséget veszített, ha pedig a BP, akkor viszont a BP 90 lehetőséget nyer.

Most nézzünk meg még egy párt: a PP és az NP-t ugyanúgy, mint azt a legjobbakkal tettük:

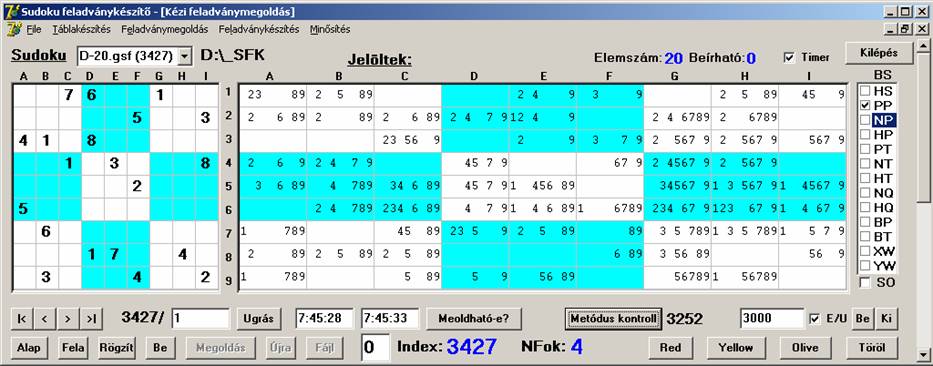
Ez egy 95%-os eredmény.

Ez egy sokkal szerényebb, csak 12% körüli

Most nézzük az együttes hatásukat, amikor az NP lesz később kiértékelve:

Ez 16%, ami 4%-os javulást jelent. Most pedig nézzük fordítva:

Itt minimális a csökkenés az egyedüli (PP) vizsgálathoz képest.

Végül nézzünk még egy esetet. Mi történik, ha a három érintett metódus a PP, NP és a HP. Mivel a HP-t még nem láttuk önmaga, először ezt nézzük meg:

Ha a HP értékelődik ki utoljára, akkor ezt látjuk:

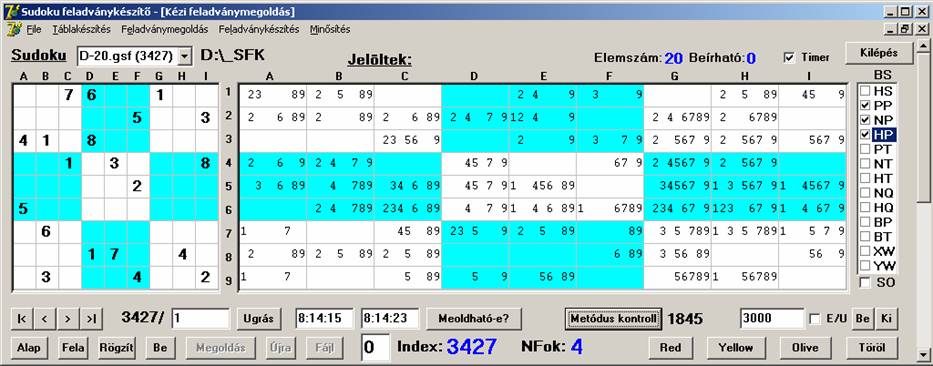
Ha a háromból a PP lesz az utolsó, akkor ezt az eredményt kapjuk:

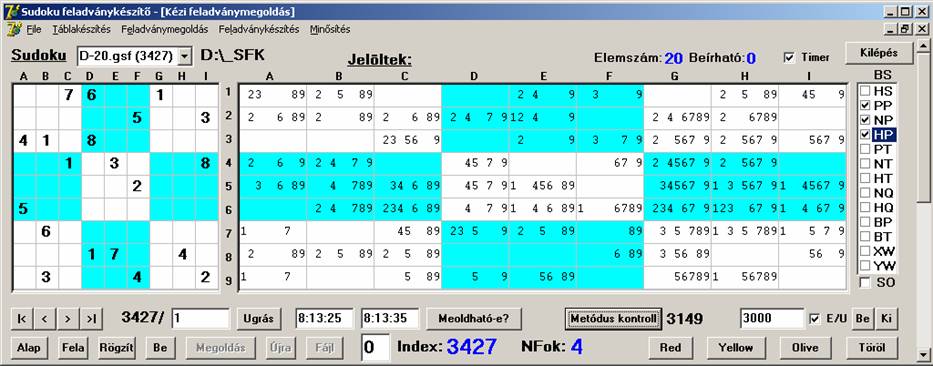
Látható, hogy ha a PP-t hagyjuk utolsónak, akkor sokkal jobban járunk, mintha a HP-t. És az is látható, hogy PP önmagában hatékonyabb (fentebbiek szerint: 3252), mint a további metódusokkal. Ellenben a HP-nek jót tett a másik kettő, hiszen önmaga csak 1935 esetet produkált, a társakkal együtt viszont 1945-öt. Nem nagy javulás, de javulás.

Már ennyi vizsgálatból is leszűrhetjük a tanulságot: a metódusok között jelentős kereszthatások léteznek és még az sem mellékes, hogy egy feladványon milyen sorrend szerint történik a kiértékelés.

Még egy felvetés a metódusokkal kapcsolatban. Miért van rájuk szükség, hiszen ott a BackTrak algoritmus, azzal minden megoldható feladvány biztosan megoldható, miért nem azt használjuk. Ennek roppant egyszerű oka van, mert nagyon lassú. Ennek érzékeltetésére bemutatnék egy feladványt. Tekintsük a 18-A.gsf (83950) adatbázis 34-edik feladványát:

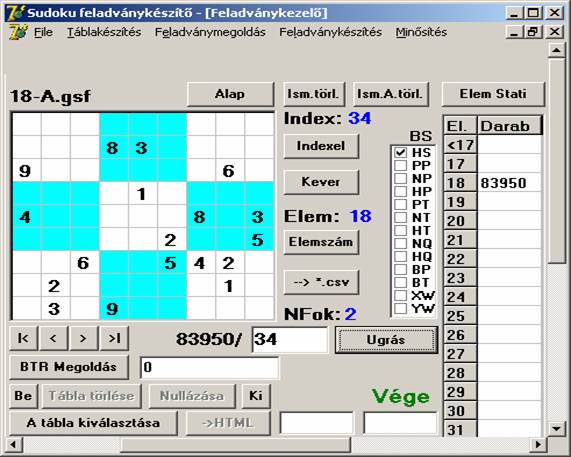
Ez a feladvány az SH segítségével a másodperc töredéke alatt megoldható:

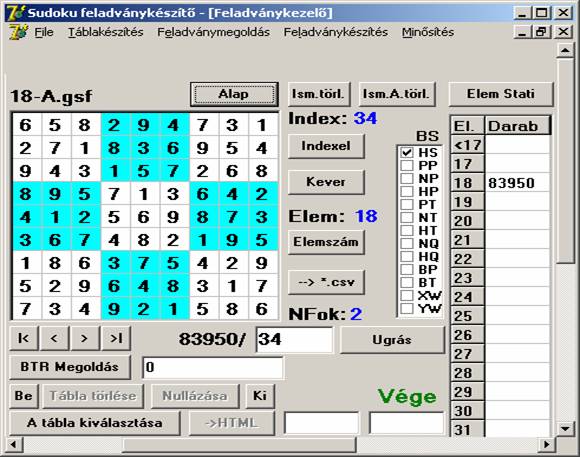
Nézzük meddig tart mindez a BackTrak algoritmusnak:

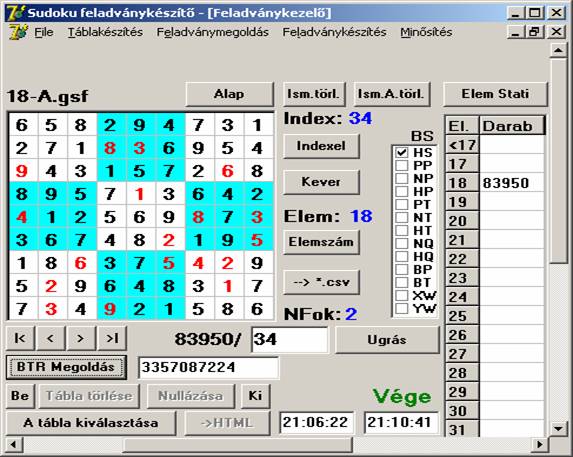
Jól látható, hogy a BTR-nek 3.357.087.224 elemi lépésre (egy szám beírása egy helyre) és 259 másodpercre volt szüksége. A BTR-t tehát csak ott és csak akkor szabad használni, ahol az elkerülhetetlen. Egyébként a 83950 feladványból csak az első 34-et teszteltem (valószínű, hogy még hosszabb futási idejű is van köztük). A többségét 1-10 másodperc alatt megoldotta a BTR, de volt még 33 és 69 másodperces futási idejű is. Egy feladvány generálásánál másodpercenként több százszor kell a feladványkezdeményt megpróbálni megoldani a feladványkészítőnek ahhoz, hogy értelmes idő alatt feladványt tudjon előállítani. Belátható, hogy ehhez a BTR teljes mértékben alkalmatlan, kellenek a megfelelően megválasztott metódusok.

A BTR rutinja:

Function Utkozik(TT: TTomb; H: Word): Boolean;  //BTR-nek
Var I: Word;
Begin
Utkozik:= False; If TT[H]=0 Then Begin Utkozik:= False; Exit End;
For I:= 1 To 20 Do If TT[H]=TT[SzT[H,I]] Then Begin Utkozik:= True; Exit End;
End;

procedure BTR;
Var I: Word;
    L, LMax: Int64;
begin
LMax:= 10000000000;
  SC:= SM;
  I:= 1; L:= 0; //novekvo normal
While (I In [1..MX]) And (L<=LMax) Do
Begin
    Inc(L); If L>LMax Then L:= 1;
If (L Mod 10000000=0) Then Begin edN.Text:= IntToStr(L); edN.RePaint End;
While SC[I]>0 Do Inc(I); Inc(SM[I]);
If SM[I]>Max Then Begin SM[I]:= 0; Dec(I); While SC[I]>0 Do Dec(I) End
Else If Not Utkozik(SM,I) Then Begin Inc(I); While SC[I]>0 Do Inc(I) End;
End;
  SA:= SM;
end;