Feladványok minősítése

A feladványokat megoldhatósági nehézségük szerint minősíteni lehet. Általában néhány csoportba szokták sorolni ebből a szempontból a feladványokat. Én egy százas skála szerinti osztályozást alkalmazok. Ezen belül a következő fő csoportokat használom:

A csoport: 1-es szint,

B csoport: 2-es szint,

C csoport: 3-5-ös szint,

D csoport: 6-9-es szint,

E csoport: 10-13-a szint és

F csoport: 13-asnál magasabb szint.

A D.gsf (10704) adatbázis feladványinak minősítési összesítését a következő képernyőn láthatjuk:

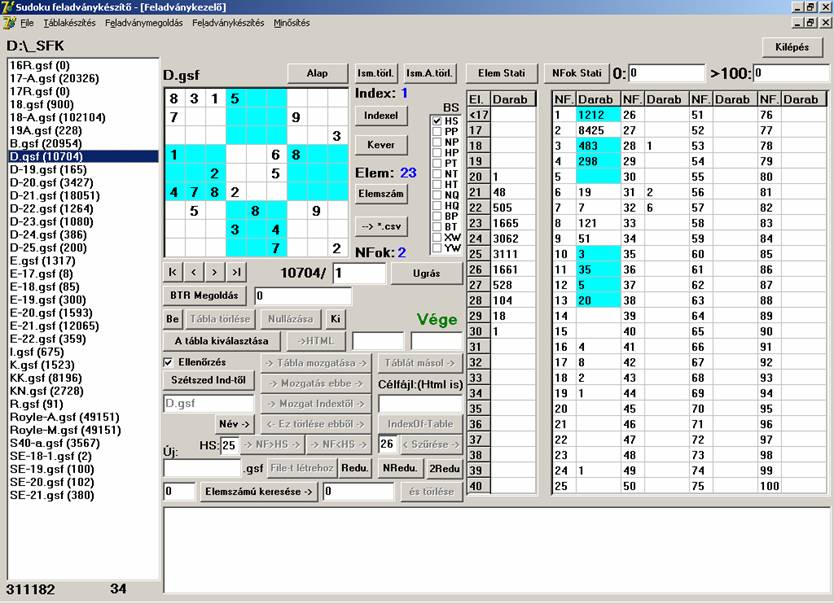
Látható, hogy a feladványok 78%-a 2-es minősítésű. Ez azért van így, mert a 2-es nehézségű feladványok előállításában csak HS metódust használunk, és mivel ez gyors is, hatékony is, a legkönnyebben az ilyen feladványok jönnek létre. A jobboldali táblázatban fehér és zöldeskék háttérszín választja el egymástól a különböző csoportokat. 100-asnál magasabb nehézségi fokú feladványt az adatbázis nem tartalmaz.

A feladványok minősítését úgy állapítom meg, hogy megoldása során hányszor és milyen típusú metódusokat kell használni. A metódusokat a minősítő a képernyőn látható sorrend szerint alkalmazza, ha az a megoldáshoz szükséges, vagyis a feladványhoz kapcsolt jelölttábla az alkalmazás révén kevesebb jelöltet tartalmaz. Minden újabb metódus növeli a minősítési értéket. Az 1-es minősítésű feladványok csak BS segítségével megoldhatók, a 2-es minősítésűekhez HS szükséges, a 3-as minősítéshez NP és így tovább. A 13-nál nagyobb értékek úgy jönnek létre, hogy a sorban hátrább álló metódusokat többször is kell alkalmazni.

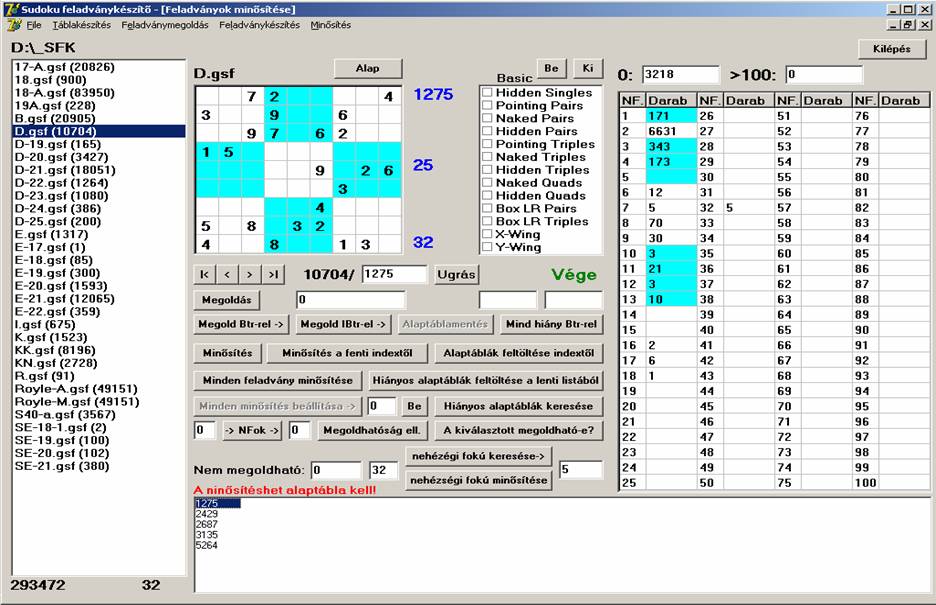
Azt szokták mondani, hogy minél kevesebb elemet tartalmaz egy feladvány, annál nehezebb megoldani. Ez igaz is meg nem is. Ha a nehézségbe beszámítjuk a megoldási időt (kézit), akkor már több igazság van a dologban. De lehet olyan feladványt készíteni, amely 18 elemű és 1-es nehézségű, de lehet olyat is, amely 28 elemű és 92-es nehézségű. Az 1275. feladvány például 32-es nehézségű és 25 elemű:

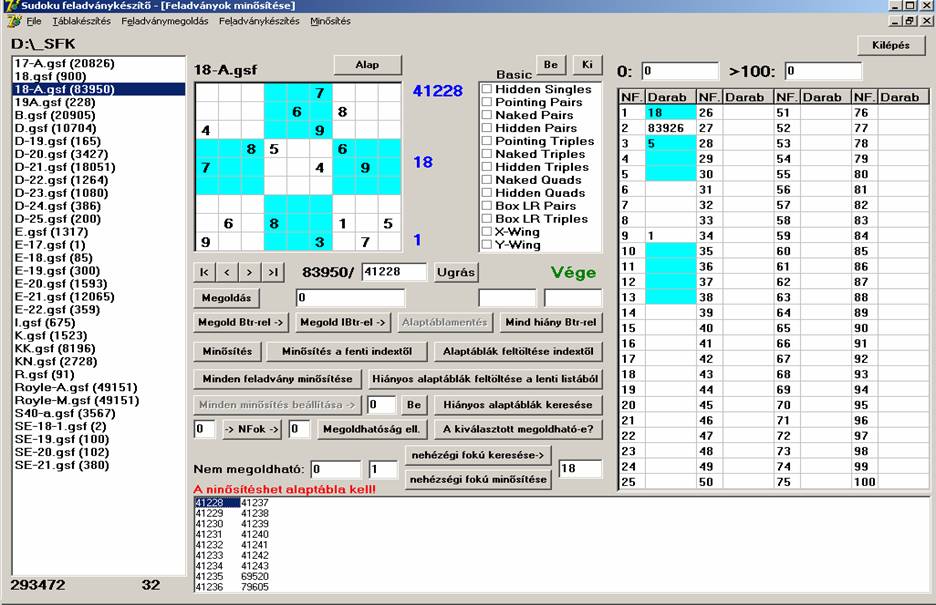
Ugyanakkor a 18-A.gsf (83950) adatbázis 41228-as feladványa 1-es nehézségi fokú:

A metódusokat elemző lapon láthattuk, hogy nagy különbségek vannak a metódusok végrehajtási ideje között. Ha például nehéz feladványokat szeretnénk készíteni, akkor a generáláskor a nehézkes, ritkán eredményes metódusokat is alkalmazni kell, mely a futási időt lelassítja, ugyanakkor egy adott feladvány előállításához nem is biztos, hogy szükségesek, egyszerűen eredménytelenségük miatt kimaradnak.

Ahhoz, hogy minél nagyobb százalékban kapjunk a generálás során nehéz feladványokat, ki kell hagyni a metódusokat a generálásból. Helyette a BackTrack eljárást kell alkalmazni, ami szintén nem gyors, de jobb eredménnyel kecsegtet. Az egyszerű BTR megoldás esetében viszont felmerülhet a gyanú, hogy a feladvány, amit a BTR jónak lát nem is az. Mert igaz, hogy ad egy megoldást a feladványra, de mi van, ha másik megoldás is van? Ekkor ugyebár a feladvány nem szabályos, azaz nem feladvány.

Meg kell tehát oldani azt a problémát, hogy egy feladvány helyes-e? Ezt BTR segítségével a következőképpen tehetjük meg:

– fusson a feltöltés BTR-el, ameddig csak lehet,

– ha nem ér a végére, akkor nem jó a feladvány, nincs egyetlen teljes kitöltés sem,

– ha végére ér kitölthető, de nem biztos, hogy egyértelműen, ezért továbblép a keresésben,

– ha már másodjára nem ér végig, akkor jó a feladvány,

– ha újra végigér, akkor nem jó, mert legalább kétféleképpen kitölthető.

Ezzel a módszerrel minden feladványról eldönthető, hogy helyes-e vagy nem, azaz megoldható-e.