Sudoku tábla
Feladat: állítsunk elő 9 x 9-es Sudoku táblát php segítségével. A Sudoku tábla olyan latin négyzet, melyben 3 x 3 darab 3 x 3-as négyzetben sem ismétlődhetnek a számok. Egy helyesen kitöltött Sudoku tábla látható a következő screenshot-on:
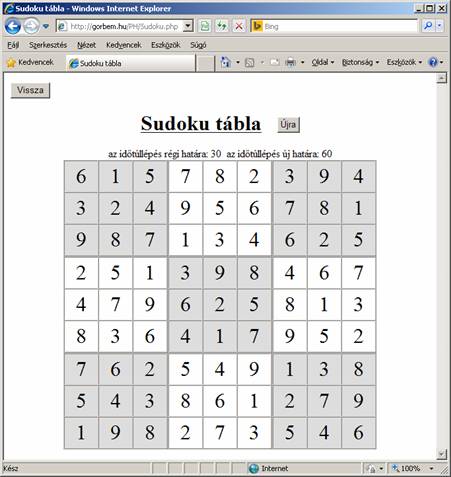
A programban a Sudoku táblát a $tomb nevű 9 x 9-es kétdimenziós tömbben tároljuk. A tárolás nem a látvány szerint történik. A tömb első sorában az bal felső 3 x 3-as négyzet elemeit, a másodikban a középső felső, a harmadikban a jobb felső és így tovább, a kilencedik sorában a jobb alsó 3 x 3-as négyzet elemeit. A rendezés az ütközésmentesítő algoritmus segítségével történik. Az elemek cserélgetésekor az egy kis (3 x 3-as) négyzetben lévő elemek a nekik megfelelő tömbsorban maradnak, csak a sorrendjük változik. Az ütközések számolása a kis négyzeten belül és a nagy négyzet sorai szerint is megtörténik. A script futási ideje nagyobb, mint a WEB helyen megengedett 30-as érték, ezért elsőként ennek az értéknek a 60-ra állítását hajtja végre a PHP kód.
Kezdetben a 9 x 9-es tömbben a számokat növekedő sorrendben helyezzük el. Ennek a táblában való megjelenését mutatja a következő screenshot:
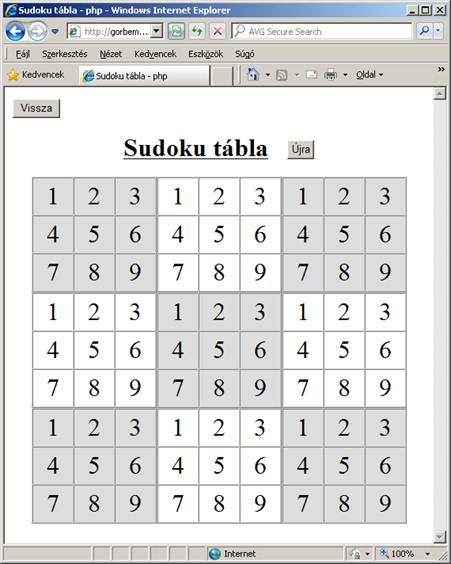
Ezek után 200 darab véletlen cserével megkeverjük a számok sorrendjét, majd az ütközésmentesítő algoritmussal addig rendezzük, amíg hibátlan Sudoku táblát nem kapunk. Az egész osztásra, az elemek cseréjére, az ütközések számolására és a képernyőn való megjelenítésre függvényeket írtam. Íme, a program listája:
http://gorbem.hu/Sudoku/SudokuTbl.php
<html>
<head>
<title>Sudoku tábla</title>
</head>
<body>
<form name="" action="Sudoku.htm" method="POST">
<input type="submit" name="vissza" value="Vissza" />
</form>
<center>
<form name="" action="Sudoku.php" method="POST">
<h1><u>Sudoku tábla</u>
<input type="submit" name="ujra" value="Újra" />
</h1>
</form>
<?php
$regi =
ini_set('max_execution_time',60);
print "az időtúllépés
régi határa: $regi ";
$uj =
ini_get('max_execution_time');
print "az időtúllépés
új határa: $uj";
function div($a,$b){
$d = round(($a-$a%$b)/$b);
return $d;
}
function csere($tomb,$i,$s1,$s2){
$p = $tomb[$i][$s1];
$tomb[$i][$s1] = $tomb[$i][$s2];
$tomb[$i][$s2] = $p;
return $tomb[$i];
}
function utkozes($tomb){
$utkoz = 0;
$p = array( array() );
for ($k=1; $k<=9; $k++){
$j = div(($k-1),3)+1;
$m = 3*$j-2;
for ($i=1; $i<=3; $i++){
$p[$k][$i] = $tomb[$j][$i+3*($k-$m)];
}
for ($i=4; $i<=6; $i++){
$p[$k][$i] = $tomb[$j+3][$i+3*($k-$m)-3];
}
for ($i=7; $i<=9; $i++){
$p[$k][$i] = $tomb[$j+6][$i+3*($k-$m)-6];
}
}
for ($i=1; $i<=9; $i++){
for ($j=1; $j<=9; $j++){
for ($k=1; $k<=9; $k++){
if ( ($k !== $i) && ($p[$k][$j] == $p[$i][$j]) ){
$utkoz++;
}
}
for ($k=1; $k<=9; $k++){
if ( ($k !== $j) && ($p[$i][$k] == $p[$i][$j]) ){
$utkoz++;
}
}
}
}
return $utkoz;
}
function kepre($tomb){
print "<table border=\"0\"
cellpadding=\"0\" cellspacing=\"0\" >\n";
for ($k=0; $k<3; $k++){
print "<tr>";
for ($l=0; $l<3; $l++){
print "<td>";
print "<table border=\"1\"
cellpadding=\"5\" cellspacing=\"0\" >\n";
for ($i=0; $i<3; $i++){
print "<tr>";
for ($j=0; $j<3; $j++){
if ( ($k+$l)%2 == 1 ){
print "<td width=\"40\"
align=\"center\"><font size=\"6\">".$tomb[3*$l+$k+1][3*$i+$j+1]."</td>";
}
else{
print "<td width=\"40\"
align=\"center\" bgcolor=\"#dddddd\"><font
size=\"6\">".$tomb[3*$l+$k+1][3*$i+$j+1]."</td>";
}
}
print "</tr>";
}
print "</table>\n";
print "</td>";
}
print "</tr>";
}
print "</table>";
return true;
}
$tomb = array( array() );
//tömbfeltöltés
for ($i=1; $i<=9; $i++){
for ($j=1; $j<=9; $j++){
$tomb[$i][$j] = $j;
}
}
//keverés
for ($i=1; $i<=9; $i++){
for ($j= 0; $j<200; $j++){
$s1 = rand(1,9);
$s2 = rand(1,9);
$tomb[$i] = csere($tomb,$i,$s1,$s2);
}
}
//rendezés ütközésmentesítéssel
$ut = utkozes($tomb);
while ($ut !== 0){
$i = rand(1,9);
$s1 = rand(1,9);
$s2 = rand(1,9);
$el = utkozes($tomb);
$tomb[$i] = csere($tomb,$i,$s1,$s2);
$ut = utkozes($tomb);
if ($ut>$el){
$tomb[$i] = csere($tomb,$i,$s1,$s2);
$ut = utkozes($tomb);
}
}
kepre($tomb);
?>
</center>
</body>
</html>