A Graph Unit használata
Turbo Pascalban a grafikus képernyő használatát többek
között a Borland Grafikus Interfészek, a *.bgi
meghajtó programok biztosítják, melyeket a Tp\Bgi mappában helyeztek el. Ezek
között találunk Hercules monitorra, színes, grafikus adapterre, EGA-ra,
IBM8514-re írt csomagokat. Számunkra a legjobb meghajtó program az EGAVGA.BGI lesz. Ez alapból 640*480-as
felbontást biztosít, 16 szín mellett. Win98-ig létezett még ennél is nagyobb
felbontást biztosító svga256.bgi, de ezt a mai gépeken már eléggé reménytelen
vállalkozás aktiválni. Pontosabban a gépeken belül a grafikus kártyák azok,
amelyek felelősek a grafikus felület *.bgi-kel való kezelhetetlenségéért. Ha
telepítéskor eltekintenénk a grafikus kártya meghajtó programjainak
telepítésétől, akkor még némi remény lehetne ezek használatára, de ekkor a
Windows grafikus képességeit jelentősen csorbítanánk, ami ugye nem lenne igazán
nyerő dolog.
XP alatt és a legújabb grafikus kártyákon a BGI
grafikát csak emulációval használhatjuk. Én a DOSBox programot szoktam erre
használni. Az emulálás miatt elég lassú, de statikus grafikus kimenetekre, az
alapok megismerésére még épp alkalmas. A DOSBox 0.73 egy ingyenes program, mely
a Net-ről letölthető, telepítő állománya önkicsomagoló, az asztalon létrehozza
az indító parancsikonját:

Erre kattintva a következőket láthatjuk:
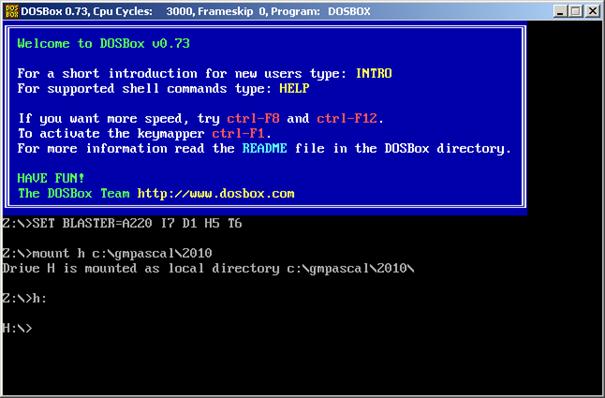
A mount h
c:\gmpascal\2010 parancsot már nekünk kell kiadni. A h jelenti majd a létrehozandó
H:\ logikai meghajtót (olyan betűt válasszunk, amilyen betűjelű meghajtó a
környezetben még nincs), a c:\gmpascal\2010 pedig azt a helyet jelöli, ahol a
DOS-os környezetben futtatható, ez esetben grafikai programunk *.exe állománya található.
H:+Enter-rel váltsunk át a
létrehozott meghajtóra. A program futtatása: a program nevének beírása a
parancssorba, majd Enter.
Írjunk
programot, mely a Turbo Pascal Graph Unitjában megtalálható legfontosabb
rajzeszközök használatát mutatja be.
Programunk neve GrDemo
lesz. A szokásos Unitok mellett a Graph
unitot is használatba kell venni. Írjunk egy GrInit nevű eljárást, mely végrehajtja a szükséges inicializálást.
A grafikus környezetet egy grafikus driver (program, illetve kártya) és annak
működtetési módja (felbontása, színhasználata) határozza meg. Mindkettő egy-egy
egész számmal jellemezhető. Jelöljük ezeket: Gd és Gm-el. Egyszerű esetekben, egy
bevezető programban, még azt sem kell feltétlen tudni, hogy ezek milyen egész
értékeket vehetnek fel. A grafikus driver lekérdezésére a Detect függvény, az inicializálásra az InitGraph eljárás használható. Ezek szintaxisa a listából
kiolvasható. A GraphResult a grafika
inicializálásakor bekövetkezett esetleges hibákra utal, ha 0 az értéke, akkor az
inicializálás sikeres.
A grafikus képernyő pontjainak koordinátái integer
típusúak, azaz a címezhető pixeltartomány, mindkét koordinátára kb. -32 ezertől
+32 ezerig tart (pontosabban -MaxInt-1-től +MaxInt-ig, ahol MaxInt=32767). A
látható tartomány, tehát ami ebből a képernyőre esik, ennek csak töredéke, még
ha a Windows-os környezetben igen jónak mondható 2048*1536-os felbontásra is
gondolunk. A Graph unitot úgy írták meg, hogy a képernyőre nem kerülő pontokat
egyáltalán nem kezeli, nem helyezi át látható helyre, nem ad hibaüzenetet, csak
egyszerűen figyelmen kívül hagyja (grafikában ez a vágás). Még ha konkrétan nem
is tudjuk, hogy mekkora felbontás áll rendelkezésünkre, sok mindent a unitra
hagyatkozva rajzolgathatunk. Lássuk hogyan. Először is lekérdezhetjük a látható
pontok X koordinátájának legnagyobb értékét, erre alkalmas GetMaxX függvény. Ugyanez az Y koordinátára a GetMaxY. Tároljuk ezeket az Xm illetve az Ym változókban. Nagyon
hasznos lehet a képernyő közepén lévő pont két koordinátájának ismerete. Ezeket
egész osztással kapjuk és tároljuk az Xk, Yk változókban. Gondolatban osszuk
fel a képernyőt ezek segítségével négy részre. A bal felső negyedben pontokat,
a jobb felsőben szakaszokat, a bal alsóban téglalap alakú kereteket, míg a jobb
alsóban maximum 40 pixel sugarú köröket rajzolunk véletlen paraméterekkel
(koordinátákkal, méretekkel és színekkel). Lássuk a programunk listájának első
részét (több szakasza lesz):
Program GrDemo;
Uses NewDelay, Crt, CrtPlus, Graph;
Var Xm,Ym, Xk,Yk, X, I: Integer;
Procedure GrInit;
Var Gd,Gm: Integer;
Begin
Gd:= Detect; InitGraph(Gd,Gm,'C:\Tp\Bgi');
If
GraphResult<>0 Then Halt;
Xm:= GetMaxX; Ym:= GetMaxY;
Xk:= Xm Div
2; Yk:= Ym Div 2;
End;
Begin
GrInit;
Randomize;
Repeat
PutPixel(Random(Xk),Random(Yk),Random(16));
SetColor(Random(16));
Line(Xk+Random(Xk),Random(Yk),Xk+Random(Xk),Random(Yk));
Rectangle(Random(Xk),Yk+Random(Yk),
Random(Xk),Yk+Random(Yk));
Circle(Xk+Random(Xk)+40,Yk+Random(Xk)+40,Random(40));
Until
KeyPressed;
CloseGraph;
End.
Egy pillanatban pedig így néz ki a futási kép:

A
programban használt további eljárások és függvények:
- PutPixel: egy pont (pixel) színének
beállítása. Három paramétere van, az első kettő a pont helyének két (X,Y)
koordinátája, a harmadik a pont színe a végrehajtás után.
- SetColor: a rajzolás színének
beállítása, egyparaméteres, a paraméter a szín neve, vagy kódja. A szín
beállítása után a több pontból álló alakzatok pontjai (határoló pontjai) ilyen
színűek lesznek.
- Line: szakaszrajzolás. Négyparaméteres
eljárás, a paraméterek a két végpont két-két koordinátája X-Y sorrendben.
- Rectangle: keretrajzolás. Téglalap
alakú, vízszintes és függőleges oldalakkal rendelkező keret. Négyparaméterű: a
bal felső és jobb alsó csúcsainak két-két koordinátája.
- Circle: körrajzolás. Háromparaméterű,
az első kettő a középpont két koordinátája, a harmadik a kör sugara.
- CloseGraph: a grafikus képernyő
bezárása, mely során törlődik a grafikus képernyő tartalma.
Ez utóbbi eljárást hagyjuk a mindenkori
programállapotban az utolsó eljáráshívásnak, a második fázisban ez előtt kell a
következő sorokat elhelyezni:
...
KeyEmpty;
ClearDevice;
Repeat
SetFillStyle(Random(8),Random(16));
SetColor(Random(16));
FillEllipse(Random(Xm), Random(Ym),
Random(80),Random(80));
Delay(100);
Until KeyPressed;
...
Az
új sorok magyarázata:
- KeyEmpty: CrtPlus eljárás, törli a
billentyűzet-puffer tartalmát, előkészítve a következő Repeat-Until szakaszt.
- ClearDevice: törli a grafikus képernyőt.
- SetFillStyle: a zárt grafikus elemek
belsejének feltöltését beállító eljárás. Kétparaméteres, az első a feltöltés
mintázatát adja, a második a belső rajzelemek színét. A 0-ás mintázat (ami
valójában nem is minta) a háttért jelenti, az 1-es a sima feltöltést (solid), a
többi valóban mintás, vonalakkal megoldva.
- FillEllipse: belsejében feltöltést
tartalmazó, teljes ellipszis rajzolása. A körvonal színét a SetColor állítja
be. Az ellipszis tengelyei függőleges és vízszintes irányúak (ferde nem lehet).
Négyparaméteres eljárás, az első kettő az ellipszis középpontját határozza meg,
a harmadik az X irányú főtengely hosszának a fele, a negyedik az Y irányúnak.
- Delay(100): egytized másodperces
várakozás, ha egyébként is lassan változik a kép, akkor elhagyható.
És a futtatás egy pillanata:
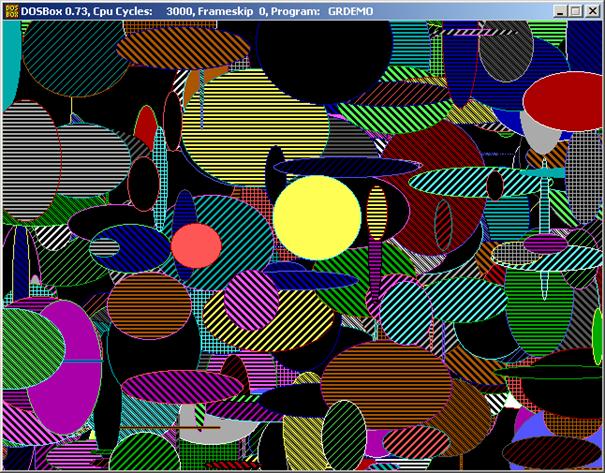
A következő szakaszban rajzoljunk koncentrikus,
különböző színű köröket a képernyő közepére. Előtte a képernyőt állítsuk be
véletlen egyszínű háttérként. Szúrjuk be a következő sorokat a CloseGraph
eljárás elé:
...
KeyEmpty;
SetFillStyle(1,Random(16));
Bar(0,0, Xm,Ym);
Varj;
For
I:= 0 To 220 Do
Begin SetColor(I); Circle(Xk,Yk,I) End;
Varj;
...
Az
új sor magyarázata:
- Bar: feltöltött téglalap rajzolása, az
aktuális fillezési eljárással és színnel. Négy paramétere van, a szokásos
csúcsok két-két koordinátája. Ebben a helyzetben a képernyőnek a háttérszínét
(feketét) takarjuk el vele, és majd erre rajzolunk.
A többi sor nem grafika-specifikus, vagy a fentiekből
már ismert. Nézzük mi lehet ennek a szakasznak a futtatási képe:
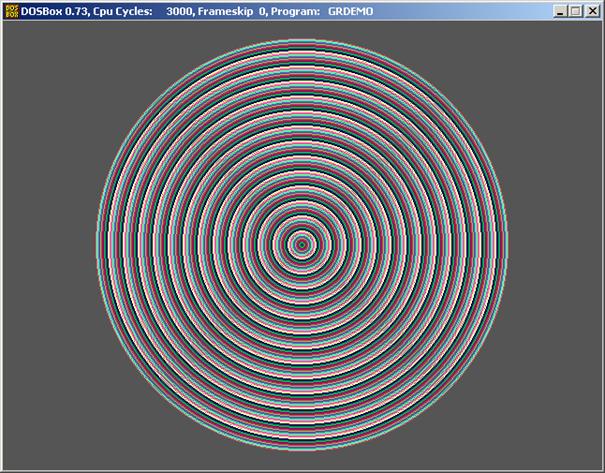
A
következő kódrészlet két kör közös részének fillezését mutatja be:
...
SetFillStyle(1,14);
Bar(0,0, Xm,Ym);
SetFillStyle(1,12);
SetColor(1);
Circle(Xk-50,Yk,100);
Circle(Xk+50,Yk,100);
Varj;
FloodFill(Xk,Yk,1);
Varj;
...
Az
új eljárás:
- FloodFill: területfeltöltés az aktuális
színnel és mintázattal. Háromparaméteres eljárás. Az első két paraméter egy
olyan pontnak a két koordinátája, amely a fillezendő terület belsejében van. A
harmadik egy színkód, amilyen színt ide beírunk, az olyan színnel körbevett
tartományt tölti fel. Ha a tartomány nem zárt, akkor lehetséges, hogy az egész
képernyő filleződik.
És
az eredmény:
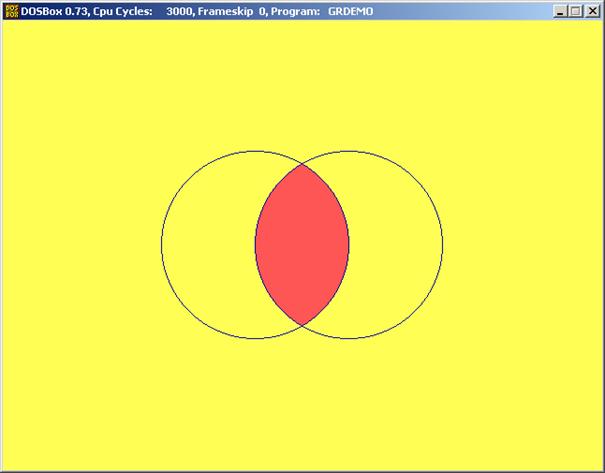
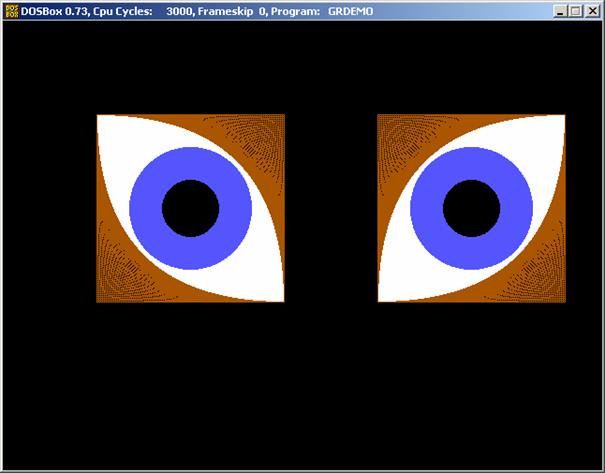
Most lássuk vonalak segítségével, hogyan lehet
burkológörbét létrehozni. Egy kis kiegészítéssel pedig figyelő szempárt. Ismét
a CloseGraph elé szúrjuk be:
...
ClearDevice;
SetColor(6);
For
I:= 0 To 200 Do If Not Odd(I) Then
Begin
Line(100+I,100, 300,100+I);
Line(100,100+I, 100+I,300);
End;
SetColor(15);
SetFillStyle(1,15); FloodFill(200,200,6);
SetColor(9);
SetFillStyle(1,9); FillEllipse(200,200,65,65);
SetColor(0);
SetFillStyle(1,0); FillEllipse(200,200,30,30);
For
I:= 0 To 200 Do If Not Odd(I) Then
Begin
Line(400,300-I, 400+I,100);
Line(400+I,300, 600,300-I);
End;
SetColor(15);
SetFillStyle(1,15); FloodFill(500,200,6);
SetColor(9);
SetFillStyle(1,9); FillEllipse(500,200,65,65);
SetColor(0);
SetFillStyle(1,0); FillEllipse(500,200,30,30);
Varj;
...
Nézzük mit kaptunk:
Az előző képekből a képernyő pixelben mért valós
méreteire már lehet következtetni. Ezekből felbátorodva, néhány feltöltött
téglalapot, illetve a 3d-s párját rajzoljunk a képernyőre, előtte azonban fehér
téglalappal takarjuk el a hátteret. Újra a szokásos helyre szúrjuk be a
következő sorokat:
...
SetFillStyle(1,15);
Bar(0,0, Xm,Ym);
SetFillStyle(1,3);
Bar(100,100, 300,400);
SetFillStyle(2,5);
Bar(400,100, 600,400);
Varj;
SetFillStyle(1,15);
Bar(0,0, Xm,Ym);
SetFillStyle(1,3);
Bar3d(100,100, 300,400,20,False);
SetFillStyle(2,5);
Bar3d(400,100, 600,400,20,True);
Varj;
Az
új eljárás magyarázata:
- Bar3d: a három-dimenziót érzékeltető
hasáb. Hatparaméteres. Az első négy a Bar eljáráséval megegyező értelmű. Az
ötödik paraméter a térbeliséget megjelenítő mélységet adja meg, míg a hatodik
arról dönt, hogy a felső téglalap körbe legyen-e rajzolva vagy sem. Ennek a
hasábok egymás fölé helyezésénél van jelentősége (a nem látszó éleket nem
rajzolja).
Lássuk a két futtatási képet, első a síkbeli fillezett
téglalapok:

A
második a térhatású hasábok:

Demonstrációs programunk utolsó fázisában egy kört
fogunk mozgatni a képernyő bal széléről indulva a jobb széléig, közben a
képernyő tetején a „Grafikus Demo Program” felírat lesz látható. Ennek a kódját
is a szokásos helyre írjuk.
...
ClearDevice;
SetColor(Yellow);
SetTextStyle(0,0,3);
OutTextXY(10,100,’Grafikus
Demo’);
OutTextXY(100,150,’Program’);
X:= 50;
For
I:= 1 To 140 Do
Begin
SetColor(5); SetFillStyle(1,5); FillEllipse(X,Yk,20,20);
Delay(100);
SetColor(0); SetFillStyle(1,0);
FillEllipse(X,Yk,20,20);
Inc(X,4);
End;
SetColor(5);
SetFillStyle(1,5); FillEllipse(X,Yk,20,20);
Varj;
Először nézzük az új eljárásokat:
- SetTextStyle: szöveg stílusának
beállítása. Háromparaméteres eljárás. Az első paraméter a fontkészlet
kiválasztására szolgál (a DOSBox alatt eléggé korlátozott). A másodikkal az
írás irányát adhatjuk meg (0: vízszintes, 1: függőleges). A harmadik paraméter a
betűméretet határozza meg.
- OutTextXY: szöveg kiírása a grafikus
képernyő megadható helyére (a CrtPlus WriteXY eljárásához hasonló). Az első két
paramétere a szöveg helye, bal felső csúcsának két koordinátája, harmadik a
kiírandó szöveg.
A mozgás úgy jön létre, hogy a feltöltött kört (hiszen
a két ellipszissugár egyenlő, tehát az ellipszis egy kör) felrajzoljuk egy
adott helyen, majd a háttérszínnel (0) újrarajzoljuk, ezáltal eltűnik, léptetjük
a középpontot (Inc(X,4)), az új helyen az egészet újra megismételjük. Végül a
cikluson kívül még egyszer felrajzoljuk, hogy ne tűnjön el véglegesen. És
mozgás egy pillanata:
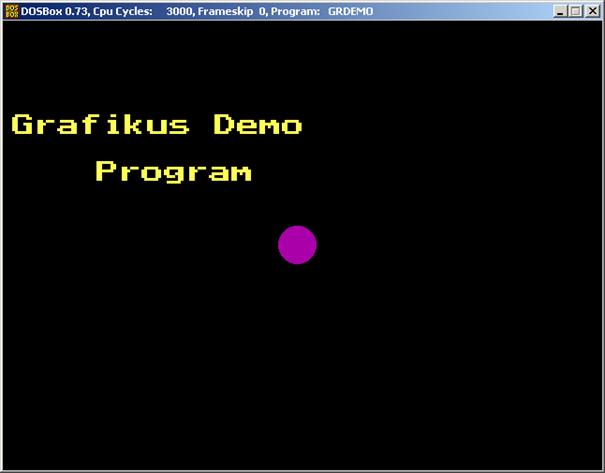
Írjunk
programot, mely egy céltáblát jelenít meg. A céltáblára lehessen lövéseket
leadni bármely billentyű megnyomásával. A lövések helyét kis fillezett körök
jelezzék (fehér területen fekete, fekete területen fehér legyen). Lövéskor
rövid hangot adjon a program. A lövések helyét véletlenül válassza a program.
Számolja a lövések számát és az elért pontokat, és ezeket folyamatosan
jelenítse meg a képernyőn. Használjuk az svga256.bgi
grafikus drivert, a legnagyobb felbontásban.
A
feladatot megoldó program listája:
Program Celtabla;
Uses
NewDelay, Crt, Graph;
Var
Gd, Gm, Xm, Ym, Xk, Yk, I, R, T, H: Integer;
D: Real;
X, Y: Longint;
Sz: String;
Ch: Char;
Begin
Gd:= InstallUserDriver('svga256',Nil); Gm:=4;
InitGraph(Gd,Gm,'C:\Tp\Bgi');
Xm:= GetMaxX; Ym:= GetMaxY;
Xk:= Xm Div
2; Yk:= Ym Div 2;
SetFillStyle(1,15);
Bar(0,0,Xm,Ym);
SetColor(0);
Circle(Xk,Yk,150);
SetFillStyle(1,0);
FloodFill(Xk,Yk,0);
R:= 0;
SetColor(15);
For
I:= 1 To 5 Do Begin Inc(R,30); Circle(Xk,Yk,R) End;
SetColor(0);
For
I:= 1 To 5 Do Begin Inc(R,30); Circle(Xk,Yk,R) End;
SetTextStyle(0,0,2);
MoveTo(Xk-10*30-5,Yk-7);
For
I:= 1 To 10 Do
Begin
MoveRel(14,0); If I=10 Then MoveRel(6,0);
Str(I,Sz); If I>5 Then SetColor(15); OutText(Sz);
End;
SetColor(0);
MoveTo(Xk+11*30-5,Yk-7);
For
I:= 1 To 9 Do
Begin
MoveRel(-46,0);
Str(I,Sz);
If
I>5 Then
SetColor(15); OutText(Sz);
End;
SetColor(0);
SetTextStyle(0,0,4);
T:= 0; Str(T,Sz);
OutTextXY(30,50,Sz);
OutTextXY(Xm-150,50,Sz);
Randomize;
For
I:= 1 To 30 Do
Begin
Ch:= Readkey; Sound(1000);
Delay(100); NoSound;
X:= Random(400)+Xk-200;
Y:= Random(400)+Yk-200;
D:= Sqrt(Sqr(X-Xk)+Sqr(Y-Yk));
If
D<150 Then
Begin
SetColor(15); SetFillStyle(1,15) End
Else
Begin
SetColor(0); SetFillStyle(1,0) End;
PieSlice(X,Y,0,360,6);
SetColor(0); SetFillStyle(1,15);
Bar(0,0,100,100);
Str(I,Sz); OutTextXY(30,50,Sz);
H:= 10-Round(Int(D/30));
If H<0 Then H:= 0; Inc(T,H);
Bar(Xm-150,50,Xm,100);
Str(T,Sz); OutTextXY(Xm-150,50,Sz);
End;
ReadKey;
End.
A program képe 15 lövés után:

Ábrázoljuk a grafikus képernyőn a
következő függvényeket:
y=0.5x+2; (egyenes)
y=x4-6x2+3; (negyedfokú
függvény)
(x+6)2+(y-3)2=4;
(kör)
y=sin(x). (Sinus görbe)
A futási kép:
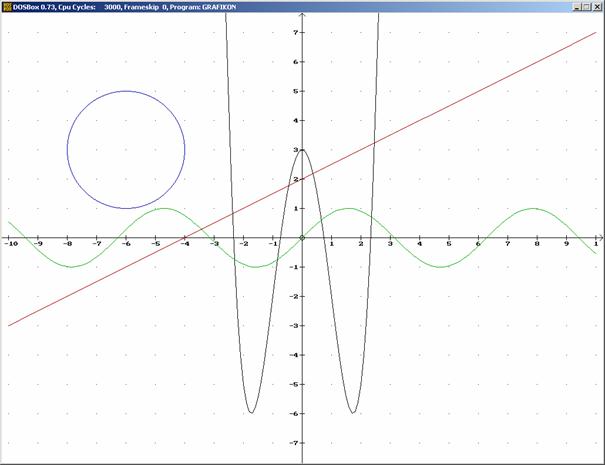
A program listája:
Program Grafikon;
Uses
NewDelay, Crt, Graph;
Const D=50;
Dx=0.1;
Var
Xm,Ym, Xk,Yk, I,J: Integer;
Sz: String;
A,B,C, X,Y: Real;
Procedure GrInit;
Var
Gd,Gm: Integer;
Begin
Gd:= InstallUserDriver('svga256',Nil); Gm:=4;
InitGraph(Gd,Gm,'C:\Tp\Bgi');
If
GraphResult<>0 Then Halt;
Xm:= GetMaxX; Ym:= GetMaxY;
Xk:= Xm Div
2; Yk:= Ym Div 2;
End;
Function PontX(R: Real): Integer;
Begin
PontX:= Round(Xk+R*D);
End;
Function PontY(R: Real): Integer;
Begin
PontY:= Round(Yk-R*D);
End;
Begin
GrInit;
SetFillStyle(1,15);
Bar(0,0, Xm,Ym);
SetColor(0);
Line(0,Yk, Xm,Yk);
Line(Xk,0, Xk,Ym);
MoveTo(Xm-5,Yk-5);
LineTo(Xm,Yk); LineTo(Xm-5,Yk+5);
MoveTo(Xk-5,5);
LineTo(Xk,0); LineTo(Xk+5,5);
Circle(Xk,Yk,4);
For
I:= -10 To 10 Do
Begin
Line(Xk+I*D,Yk-4,Xk+I*D,Yk+4);
Str(I,Sz);
If
I<0 Then
OutTextXY(Xk+I*D-7,Yk+6,Sz);
If
I>0 Then
OutTextXY(Xk+I*D-3,Yk+6,Sz)
End;
For
I:= -7 To 7 Do
Begin
Line(Xk-4,Yk-I*D,Xk+4,Yk-I*D);
Str(I,Sz);
If
I<0 Then
OutTextXY(Xk-22,Yk-I*D-4,Sz);
If
I>0 Then
OutTextXY(Xk-14,Yk-I*D-4,Sz);
End;
For
I:= -10 To 10 Do
For
J:= -7 To 7 Do PutPixel(Xk+I*D,Yk-J*D,0);
SetColor(Red);
A:= 0.5; B:= 2; {y=0.5x+2}
X:= -10; MoveTo(PontX(X),PontY(A*X+B));
Repeat
X:= X+Dx; Y:= A*X+B;
LineTo(PontX(X),PontY(Y));
Until
X>10;
SetColor(Blue); {(x+6)2+(y-3)2=4}
Circle(PontX(-6),PontY(3),2*D);
SetColor(Black);
A:= 1; B:= -6; C:= 3; {y=x4-6x2+3}
X:= -6; MoveTo(PontX(X),PontY(A*X*X*X*X+B*X*X+C));
Repeat
X:= X+Dx; Y:= A*X*X*X*X+B*X*X+C;
LineTo(PontX(X),PontY(Y));
Until
X>6;
{y=sin(x)}
SetColor(Green);
X:= -10; MoveTo(PontX(X),PontY(Sin(X)));
Repeat
X:= X+Dx; Y:= Sin(X);
LineTo(PontX(X),PontY(Y));
Until
X>10;
ReadKey;
CloseGraph;
End.
Írjunk
programot, mely a közismert Hanoi tornyai
játékot mutatja be grafikus képernyőn. A korongok áthelyezése animációs legyen,
azaz a korong induljon el az aktuális helyéről, és a valóságos mozgáshoz
hasonlóan, foglalja el az új helyét. (Aki nem ismerné: egy oszlopon egyre
csökkenő méretű korongok vannak. További két üres oszlop áll rendelkezésünkre,
hogy a korongokat egy másik oszlopra áthelyezzük. Egyszerre csak egy korongot
rakhatunk át, és az átrakás során soha nem fordulhat elő, hogy kisebb korongra
ráhelyezünk egy nagyobbat.)
A program futásának egy pillanata, ahol
kezdetben minden korong az a jelű oszlopon volt, és a
101. lépés után a program le lett állítva:
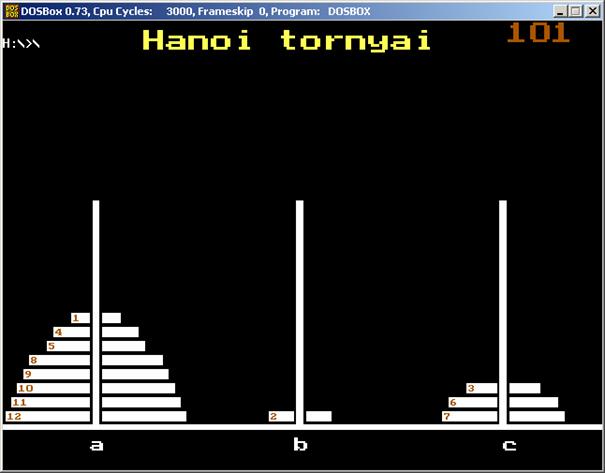
És a program listája:
Program Hanoi;
Uses NewDelay, Crt, Graph;
Const Db=12;
Var Mx, My, Gd, Gm: Integer;
Lsz: Integer;
Type TKor= Object
FX, FY, FD, FV, FS: Integer;
Procedure Init(IX, IY, ID, IV, IS: Integer);
Procedure Show;
Procedure Hide;
Procedure MoveRel(DX, DY: Integer);
Function GetX: Integer;
Function GetY: Integer;
Function GetV: Integer;
End;
Procedure TKor.Init(IX, IY, ID, IV, IS: Integer);
Begin
FX:= IX; FY:= IY; FD:= ID; FV:= IV; FS:= IS;
End;
Procedure TKor.Show;
Var Ws: String;
Begin
Bar(FX-FD, FY, FX, FY+FV);
Bar(FX+Round(0.022*Mx), FY,
FX+FD+Round(0.022*Mx), FY+FV);
SetTextStyle(0,0,1);
SetColor(6);
Str(FS, Ws);
OutTextXY(FX-FD+2,FY+2, Ws);
End;
Procedure TKor.Hide;
Begin
SetViewPort(FX-FD, FY, FX, FY+FV, ClipOn);
ClearViewPort;
SetViewPort(FX+Round(0.022*Mx), FY,
FX+FD+Round(0.022*Mx), FY+FV, ClipOn);
ClearViewPort;
SetViewPort(0, 0, Mx, My, ClipOff);
End;
Procedure TKor.MoveRel(DX, DY: Integer);
Begin
Hide; FX:= FX+DX; FY:= FY+DY; Show
End;
Function TKor.GetX: Integer;
Begin
GetX:=FX;
End;
Function TKor.GetY: Integer;
Begin
GetY:= FY;
End;
Function TKor.GetV: Integer;
Begin
GetV:=FV;
End;
Const Ac=0.144; Bc=0.484; Cc=0.824;
Var KorT: Array[1..Db] Of TKor;
Darab: Array['a'..'c'] Of Byte;
Procedure KorongAtr(N: Byte; F, G: Char);
Var E: Byte;
Ws: String;
Begin
If (F='a') And (G='b') Then E:=1;
If (F='b') And (G='c') Then E:=2;
If (F='c') And (G='a') Then E:=3;
If (F='a') And (G='c') Then E:=4;
If (F='b') And (G='a') Then E:=5;
If (F='c') And (G='b') Then E:=6;
While KorT[N].GetY>0.3*My Do KorT[N].MoveRel(0,-1);
Dec(Darab[F]);
With KorT[N] Do
Case E of
1: While GetX<Bc*Mx Do MoveRel(1,0);
2,4: While GetX<Cc*Mx Do MoveRel(1,0);
3,5: While GetX>Ac*Mx Do MoveRel(-1,0);
6: While GetX>Bc*Mx Do MoveRel(-1,0);
End;
While KorT[N].GetY<0.87*My-Darab[G]*1.5*KorT[N].GetV Do
KorT[N].MoveRel(0,1);
Inc(Darab[G]);
Inc(Lsz);
SetViewPort(Mx-100, 0, Mx, 100, ClipOn);
ClearViewPort;
SetViewPort(0, 0, Mx, My, ClipOff);
Str(Lsz,Ws);
SetTextStyle(0,0,3);
OutTextXY(Mx-100,2, Ws);
End;
Procedure ToronyAtr(N: Byte; A, B, C: Char);
Begin
If N>0 then
Begin
ToronyAtr(N-
KorongAtr(N, A, B);
ToronyAtr(N-
If KeyPressed Then Halt;
End;
End;
Procedure GrInit;
Var Gd, Gm: integer;
Begin
DetectGraph(Gd, Gm);
InitGraph(Gd, Gm, 'C:\TP\BGI');
Mx:= GetMaxX; My:= GetMaxY;
End;
Procedure Start;
Var I: Byte; X, Y, D, V, T: Integer; Ch: Char;
Begin
SetColor(14);
SetTextStyle(0,0,3);
OutTextXY(150,10, 'Hanoi tornyai');
Bar(0,Round(0.9*My),Mx,Round(0.91*My));
Bar(Round(0.15*Mx),Round(0.4*My),
Round(0.16*Mx),Round(0.9*My));
Bar(Round(0.49*Mx),Round(0.4*My),
Round(0.50*Mx),Round(0.9*My));
Bar(Round(0.83*Mx),Round(0.4*My),
Round(0.84*Mx),Round(0.9*My));
SetColor(15);
SetTextStyle(0,0,2);
OutTextXY(Round(0.146*Mx),Round(0.93*My), 'a');
OutTextXY(Round(0.486*Mx),Round(0.93*My), 'b');
OutTextXY(Round(0.836*Mx),Round(0.93*My), 'c');
For I:= 1 To Db Do
Begin
V:= Round(0.02*My);
T:= Round(1.5*V);
D:= Round((0.02+I*0.01)*Mx);
X:= Round(0.144*Mx);
Y:= Round(0.87*My-(Db-I)*T);
KorT[I].Init(X, Y, D, V, I);
KorT[I].Show;
End;
Darab['a']:= Db;
For Ch:= 'b' To 'c' Do Darab[Ch]:= 0;
End;
Begin
GrInit;
Start;
Lsz:= 0;
ToronyAtr(Db, 'a','b','c');
SetTextStyle(0,0,3);
OuttextXY(150,120,'Kész');
Readkey;
CloseGraph;
End.
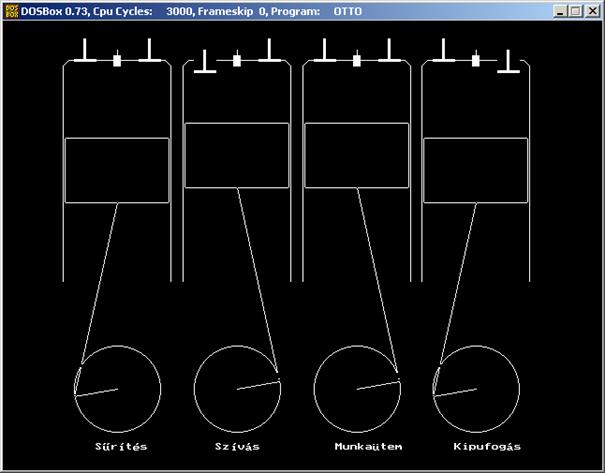
Írjunk programot mely egy négyhengeres Otto-motor működését modellezi. A modellen legyenek szelepek és
gyertyák és a megfelelő pillanatban működjenek. Minden
henger alatt tüntessük fel, hogy épp melyik fázisban van (Szívás, Sűrítés,
Munkaütem vagy Kipufogás).
A futtatás egy pillanata:
A program listája:
Program Otto;
Uses NewDelay, Crt,CrtPlus, Graph;
Const HSz=4;
Var MX, MY: Integer;
Type Henger= Object
FX, FY, FD, FS: Real;
X, Y, D, R, T: Integer;
Mf: Integer;
Procedure Init(IX, IY, ID: Real);
Procedure SetFazis(IS: Real);
Function GetSzog: Integer;
Function GetMFazis: Integer;
Procedure FrameDraw;
Procedure Show;
End;
Control= Object
HT: Array[1..Hsz] Of Henger;
F: Integer;
Procedure Init;
Procedure Run;
Procedure Done;
End;
Procedure Henger.Init(IX, IY, ID: Real);
Begin
FX:= IX; FY:= IY; FD:= ID;
X:= Round(FX*MX); Y:= Round(FY*MY); D:= Round(FD*MX);
R:= Round(0.4*D);
End;
Procedure Henger.SetFazis(IS:Real);
Begin
FS:= IS;
T:= Round(R*Sin(FS*Pi/180));
Case Round(FS) Of
0..89: Mf:=1;
90..269: Mf:=2;
270..449: Mf:=3;
450..629: Mf:=4;
630..719: Mf:=1;
End;
End;
Function Henger.GetSzog:Integer;
Begin
GetSzog:= Round(FS);
End;
Function Henger.GetMFazis: Integer;
Begin
GetMFazis:= Mf;
End;
Procedure Henger.FrameDraw;
Begin
SetWriteMode(0);
Setcolor(15);
{henger}
Moveto(X, Y+2*D);
LineTo(X, Y);
LineTo(Round(X+0.05*D), Round(Y-0.05*D));
Lineto(Round(X+0.95*D), Round(Y-0.05*D));
LineTo(X+D, Y);
LineTo(X+D, Y+2*D);
{gyertya}
SetFillStyle(1,15);
Bar(Round(X+0.47*D), Round(Y-0.1*D), Round(X+0.53*D), Y);
Line(Round(X+0.5*D), Round(Y-0.15*D), Round(X+0.5*D), Y);
{szelepek}
SetLineStyle(SolidLn, 0, ThickWidth);
Line(Round(X+0.1*D), Round(Y-0.05*D),
Round(X+0.3*D),
Round(Y-0.05*D));
Line(Round(X+0.2*D), Round(Y-0.25*D),
Round(X+0.2*D),
Round(Y-0.05*D));
Line(Round(X+0.7*D), Round(Y-0.05*D),
Round(X+0.9*D), Round(Y-0.05*D));
Line(Round(X+0.8*D), Round(Y-0.25*D),
Round(X+0.8*D), Round(Y-0.05*D));
SetLineStyle(SolidLn, 0, NormWidth);
{főtengely}
Circle(Round(X+D*0.5), Y+3*D, R);
End;
Procedure Henger.Show;
Begin
SetWriteMode(XorPut);
Rectangle(Round(X+0.02*D), Round(Y+0.1*D+0.5*D+T),
Round(X+D-0.02*D), Round(Y+0.7*D+0.5*D+T));
Line(Round(X+D*0.5),Y+3*D,
Round(X+D*0.5+R*Cos(FS*Pi/180)),
Round(Y+3*D+R*Sin(FS*Pi/180)));
Line(Round(X+D*0.5), Round(Y+D*0.7+0.5*D)+T,
Round(X+D*0.5+R*Cos(FS*Pi/180)),
Round(Y+3*D+R*Sin(FS*Pi/180)));
SetWriteMode(0);
If ((GetSzog-90) Mod 180)=0 Then
Begin
{aláírás, szelepek}
SetViewPort(X, Round(Y+3.5*D), X+D,
Round(Y+3.6*D), ClipOn);
ClearViewPort;
SetViewPort(0, 0, MX, MY, ClipOff);
Case GetMFazis of
1:Begin
SetViewPort(Round(X+0.1*D),Round(Y-0.25*D),
Round(X+0.3*D),Round(Y+0.06*D),ClipOn);
ClearViewPort;
SetViewPort(Round(X+0.7*D),Round(Y-0.25*D),
Round(X+0.9*D),Round(Y+0.06*D),ClipOn);
ClearViewPort;
SetViewPort(0, 0, MX, MY, ClipOff);
SetLineStyle(SolidLn, 0, ThickWidth);
Line(Round(X+0.1*D), Round(Y+0.05*D),
Round(X+0.3*D), Round(Y+0.05*D));
Line(Round(X+0.2*D), Round(Y-0.15*D),
Round(X+0.2*D), Round(Y+0.05*D));
line(Round(X+0.7*D), Round(Y-0.05*D),
Round(X+0.9*D), Round(Y-0.05*D));
line(Round(X+0.8*D), Round(Y-0.25*D),
Round(X+0.8*D), Round(Y-0.05*D));
SetLineStyle(SolidLn, 0, NormWidth);
OutTextXY(Round(X+0.3*D), Round(Y+3.5*D), 'Szívás')
End;
2:Begin
SetViewPort(Round(X+0.1*D), Round(Y-0.25*D),
Round(X+0.3*D), Round(Y+0.06*D),ClipOn);
ClearViewPort;
SetViewPort(0, 0, MX, MY, ClipOff);
SetLineStyle(SolidLn, 0, ThickWidth);
Line(Round(X+0.1*D), Round(Y-0.05*D),
Round(X+0.3*D), Round(Y-0.05*D));
Line(Round(X+0.2*D), Round(Y-0.25*D),
Round(X+0.2*D), Round(Y-0.05*D));
SetLineStyle(SolidLn, 0, NormWidth);
OutTextXY(Round(X+0.3*D), Round(Y+3.5*D), 'Sűrítés');
End;
3:Begin
OutTextXY(Round(X+0.48*D), Round(Y+0.02*D), '*');
Sound(700); Delay(30); NoSound;
SetViewPort(Round(X+0.46*D), Round(Y+0.01*D),
Round(X+0.54*D), Round(Y+0.06*D),
ClipOn);
ClearViewPort;
SetViewPort(0, 0, MX, MY, ClipOff);
OutTextXY(Round(X+0.3*D),
Round(Y+3.5*D),
'Munkaütem');
End;
4:Begin
SetViewPort(Round(X+0.1*D), Round(Y-0.25*D),
Round(X+0.3*D), Round(Y+0.06*D), ClipOn);
ClearViewPort;
SetViewPort(Round(X+0.7*D), Round(Y-0.25*D),
Round(X+0.9*D), Round(Y+0.06*D), ClipOn);
ClearViewPort;
SetViewPort(0, 0, MX, MY, ClipOff);
SetLineStyle(SolidLn, 0, ThickWidth);
Line(Round(X+0.1*D), Round(Y-0.05*D),
Round(X+0.3*D), Round(Y-0.05*D));
Line(Round(X+0.2*D), Round(Y-0.25*D),
Round(X+0.2*D), Round(Y-0.05*D));
Line(Round(X+0.7*D), Round(Y+0.05*D),
Round(X+0.9*D), Round(Y+0.05*D));
Line(Round(X+0.8*D), Round(Y-0.15*D),
Round(X+0.8*D), Round(Y+0.05*D));
SetLineStyle(SolidLn, 0, NormWidth);
OutTextXY(Round(X+0.3*D),
Round(Y+3.5*D), 'Kipufogás');
End;
End;
End;
End;
Procedure Control.Init;
Const Xt: Array[1..4] Of Real= (0.1,0.3,0.5,0.7);
Ft: Array[1..4] Of Integer= (0,540,180,360);
Var Gd, Gm, I: Integer;
Begin
DetectGraph(Gd, Gm); InitGraph(Gd, Gm, 'C:\Tp\bgi');
MX:= GetMaxX; MY:= GetMaxY;
For I:= 1 to HSz Do With HT[i] Do
Begin
Init(Xt[I],0.1,0.18); F:= Ft[I]; SetFazis(F);
FrameDraw; Show;
End;
End;
Procedure Control.Run;
Var Sd, I: Integer;
Begin
Sd:= 5;
Repeat
For I:= 1 To HSz Do With HT[I] do
Begin
Show; F:=GetSzog; Inc(F, Sd); F:=F Mod 720;
SetFazis(F); Show;
End;
Delay(12);
Until keypressed;
End;
Procedure Control.Done;
Begin
ClearDevice;
CloseGraph;
End;
Var Ctr: Control;
Begin
Ctr.Init;
Ctr.Run;
Ctr.Done;
End.
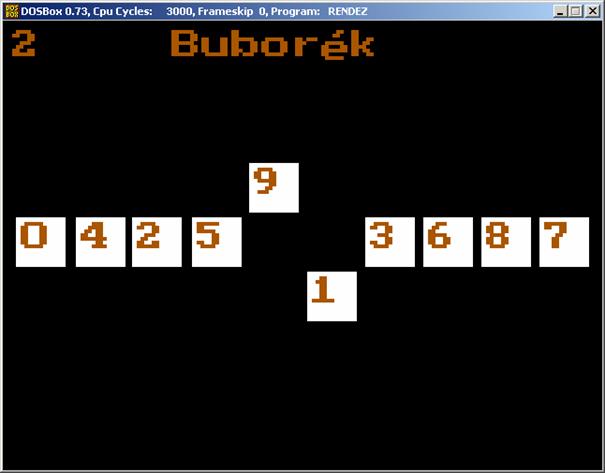
Írjunk
programot, amely a legfontosabb rendező eljárásokat szemlélteti. A számok 0..9. Minden szám egy kártyán legyen látható. A rendezés a
grafikus képernyőn megjelenő, a számokat tartalmazó lapok legyenek, és lassan
hajtsa végre (a grafika miatt túlságosan egyébként sem gyors) a cseréket,
közben számolja és jelenítse meg a lépések számát. A rendezés menüből legyen
választható. Lehessen véletlen elrendezést kérni, és ugyanolyan kiindulásból,
különböző módszerekkel rendezni, a lépések számának összehasonlíthatósága
miatt.
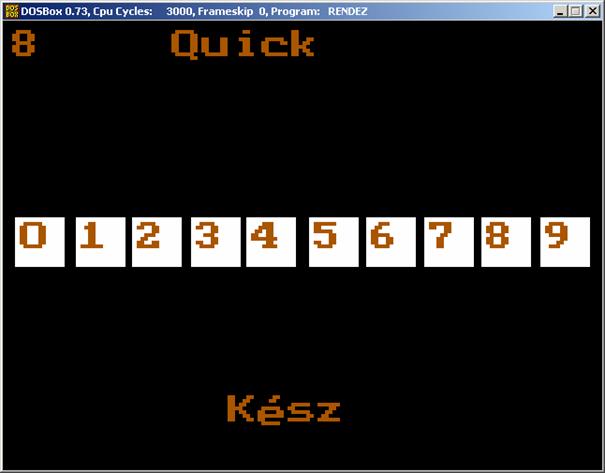
A futási képek:

Program Rendez;
Uses NewDelay, Crt, CrtPlus, Graph, Drivers;
Const Sor=210; {a
kártyasor y koord}
Lk=15; {a lapok kezdő x koord}
Db=9; {a kártyák száma-1}
Lt=62; {a lapok távolsága}
Ls=52; {a lapok szélessege és magassága}
Bm=4; {szám és betűméret}
Bx=5; {a szám helye a lapon - x koord}
By=5; {a szám helye a lapon - y koord}
Emp=1; {a
várakozási idő}
Type TLap= Object
FX, FY, FD, FS: Integer;
Procedure Init(IX, IY, ID, IS: Integer);
Procedure Show;
Procedure Hide;
Procedure MoveRel(DX, DY: Integer);
Function GetX:Integer;
Function GetY:Integer;
Function GetS:Byte;
End;
Const MSor: Array[1..10] Of String[30]=
(' Keverés ',
' Közvetlen összehasonlítással ',
' Buborék módszerrel ',
' Javított buborék módszerrel ',
' Shell rendezés ',
' Kiválasztással ',
' Beszúrással ',
' Javított beszúrással ',
' Quick rendezéssel ',
' Kilépés a programból ');
Procedure TLap.Init(IX, IY, ID, IS: Integer);
Begin
FX:= IX; FY:= IY; FD:= ID; FS:= IS;
End;
Procedure TLap.Show;
Var W: String;
Begin
Bar(GetX, GetY, GetX+FD, GetY+FD); Str(GetS, W);
SetTextStyle(0, 0, Bm);
SetColor(6); OutTextXY(GetX+Bx, FY+By, W);
End;
Procedure TLap.Hide;
Begin
SetViewPort(GetX, GetY, GetX+FD, GetY+FD, ClipOn);
ClearViewPort;
SetViewPort(0, 0, GetMaxX, GetMaxY, ClipOff);
End;
Procedure TLap.Moverel(DX, DY: Integer);
Begin
Hide; FX:= GetX + DX; FY:= GetY + DY; Show;
End;
Function TLap.GetX:Integer;
Begin
GetX:= FX;
End;
Function TLap.GetY:Integer;
Begin
GetY:= FY;
End;
Function TLap.GetS:Byte;
Begin
GetS:= FS;
End;
Var Mx, My, Sz: Integer;
Lap: Array[0..Db] Of TLap;
M, T, P: Array[0..Db] Of Byte;
I, Mp: Byte;
Kevert: Boolean;
Procedure Init;
Var Gd, Gm: integer;
Begin
Gd:= Detect; InitGraph(Gd, Gm, 'C:\Tp\Bgi');
Mx:= GetMaxX; My:= GetMAxY;
End;
Procedure Lapkepre;
Var I: Byte;
Begin
ClearDevice;
For I:= 0 To Db Do Lap[I].Init(I*Lt+Lk, Sor, Ls, P[I]);
For I:= 0 To Db Do Lap[I].Show;
End;
Procedure Keveres;
Var I, V: Byte;
Begin
Randomize;
For I:= 0 To Db Do M[I]:=0;
For I:= 0 To Db Do
Begin
Repeat
V:= Random(Db+1);
Until M[V]=0;
M[V]:= 1;
T[I]:= V;
End;
For I:= 0 To Db Do P[I]:= T[I];
End;
Procedure Csere(A, B: byte);
Var U, V: Integer;
I: Integer;
Begin
U:= Lap[A].GetX;
V:= Lap[B].GetX;
For I:= 1 To Lt Do
Begin
Lap[A].MoveRel(0,-1);
Lap[B].MoveRel(0, 1);
End;
For I:= U to V do
Begin
Lap[A].MoveRel( 1,0);
Lap[B].Moverel(-1,0);
End;
For I:= 1 To Lt Do
Begin
Lap[A].MoveRel(0, 1);
Lap[B].MoveRel(0,-1);
End;
End;
Procedure Jobbra(A: byte);
Var I: Integer;
Begin
For I:= 1 To Lt Do Lap[A].MoveRel(1,0);
End;
Procedure Le(A: Byte);
Var I: Integer;
Begin
For I:= 1 To Lt Do Lap[A].MoveRel(0,1);
End;
Procedure Balra(B: Byte);
Var I: Integer;
Begin
For I:= 1 To Lt do Lap[B].MoveRel(-1,0);
End;
Procedure Fel(B: Byte);
Var I: Integer;
Begin
For I:=1 To Lt Do Lap[B].MoveRel(0,-1);
End;
Procedure Szamol;
Var Ws: String;
Begin
Inc(Sz);
Str(Sz,Ws);
SetViewPort(0,0,100,100,ClipOn);
ClearViewPort;
SetViewPort(0,0,Mx,My,ClipOff);
OutTextXY(10,10,Ws);
End;
Procedure Kozvetlen;
Var I, J: Byte;
P: TLap;
Begin
Sz:= 0;
For I:= 0 To Db-1 Do For J:=I+1 To Db Do
If Lap[i].GetS>Lap[j].GetS Then
Begin
Csere(I,J);
P:= Lap[I];
Lap[I]:= Lap[J];
Lap[J]:= p;
Szamol;
Delay(Emp);
End;
End;
Procedure Buborek;
Var I, J: Byte;
P: TLap;
Begin
Sz:= 0;
For J:= 0 To Db-1 Do
For I:= 0 To Db-1 Do
If Lap[I].GetS>Lap[I+1].GetS Then
Begin
Csere(I,I+1);
P:= Lap[I];
Lap[I]:= Lap[I+1];
Lap[I+1]:= P;
Szamol;
Delay(Emp);
End;
End;
Procedure JBuborek;
Var I: Byte;
VoltCsere: Boolean;
P: TLap;
Begin
Sz:= 0;
While VoltCsere Do
Begin
VoltCsere:= False;
For I:= 0 To Db-1 Do
If Lap[I].GetS>Lap[I+1].GetS Then
Begin
VoltCsere:= True;
Csere(I,I+1);
P:= Lap[I];
Lap[I]:= Lap[I+1];
Lap[I+1]:= P;
Szamol;
End;
Delay(Emp);
End;
End;
Procedure Shell;
Var I, G: Byte;
VoltCsere: Boolean;
P: TLap;
Begin
Sz:= 0;
G:= (Db+1) Div 2;
Repeat
Repeat
VoltCsere:= False;
For I:=0 To Db-G Do
If Lap[I].GetS>Lap[I+G].GetS then
Begin
Csere(I,I+G);
P:= Lap[I];
Lap[I]:= Lap[I+G];
Lap[I+G]:= P;
VoltCsere:= True;
Szamol;
End;
Delay(Emp);
Until Not VoltCsere;
G:= G Div 2;
Until G=0;
End;
Procedure Kivalasztas;
Var I, J: integer;
P: TLap;
Lk, Lki: byte;
Begin
Sz:= 0;
I:= -1;
While I<Db-1 Do
Begin
Lk:= Lap[I+1].GetS; Lki:= I+1;
For J:= I+1 To db Do If Lap[J].GetS<Lk Then
Begin
Lk:= Lap[J].GetS;
Lki:= J;
End;
If I+1<>Lki Then
Begin
Csere(I+1,Lki);
P:= Lap[I+1];
Lap[I+1]:= Lap[Lki];
Lap[Lki]:= P;
Szamol;
End;
Inc(I);
Delay(Emp);
End;
End;
Procedure Beszuras;
Var I, J, K: Byte;
P: TLap;
Begin
Sz:= 0;
For I:= 1 to Db do
Begin
Le(I);
J:= I;
{Lineáris keresés}
While (J>0) And (Lap[J-1].GetS>Lap[I].GetS) Do
Begin
Jobbra(J-1);
Balra(I);
Dec(J);
Szamol;
End;
Fel(I);
P:= Lap[I];
For K:=I DownTo J Do Lap[K]:= Lap[K-1];
Lap[J]:= P;
Delay(Emp);
End;
End;
Procedure JBeszuras;
Var I, J, K: Byte;
P: TLap;
Ah, Fh, M: Byte;
Begin
Sz:= 0;
For I:= 1 To Db Do
Begin
Le(I); Ah:= 0; Fh:= I-1; J:= I;
if Lap[I].GetS<Lap[Fh].GetS Then
Begin
Repeat
{Bináris keresés}
M:= (Ah+Fh) Div 2;
If Lap[M].GetS>=Lap[I].GetS Then Fh:= M Else Ah:= M+1;
Until Ah=Fh;
While J>Fh do
Begin
Jobbra(J-1);
Balra(I);
Dec(J);
Szamol;
End;
End;
Fel(I); P:= Lap[I];
For K:=I DownTo J Do Lap[K]:= Lap[K-1];
Lap[J]:= P;
delay(Emp);
End;
End;
Procedure Quick(Ki, Vi: Integer);
Var A, F :integer;
K: integer;
P: TLap;
Begin
A:= Ki;
F:= Vi;
K:= Lap[(Ki+Vi) Div 2].GetS;
Repeat
While Lap[A].GetS<K Do Inc(A);
While Lap[F].GetS>K Do Dec(F);
If A<=F Then
Begin
If A<F Then
Begin
Csere(A, F);
P:= Lap[A];
Lap[A]:= Lap[F];
Lap[F]:= P;
Szamol;
Delay(Emp);
end;
Inc(A);
Dec(F);
End;
Until A>F;
If KI<F Then Quick(Ki,F);
If A<Vi Then Quick(A,Vi);
End;
Begin
Szinek(1,0);
ClrScr;
ShowMouse;
InitEvents;
Mp:= 1;
Repeat
If Mp=0 Then Mp:= 1;
Ablak(7,0,23,5,56,16,True,'Menü');
For I:= 1 To 10 Do WriteXY(25,5+I,MSor[I]);
Mp:= Menu(7,0,Green,25,6,30,10,Mp);
Case Mp Of
1:Begin
Init; Keveres; Lapkepre; Varj;
CloseGraph; Kevert:=True
End;
2:If Kevert Then
Begin
Init; Lapkepre; OutTextXY(180,10,'Közvetlen'); Varj;
Kozvetlen;
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
3:If Kevert Then
Begin
Init; Lapkepre; OutTextXY(180,10,'Buborék'); Varj;
Buborek;
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
4:If Kevert Then
Begin
Init;
Lapkepre; OutTextXY(180,10,'Jav.Buborék'); Varj;
JBuborek;
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
5:If Kevert Then
Begin
Init; Lapkepre; OutTextXY(180,10,'Shell'); Varj;
Shell;
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
6:If Kevert Then
Begin
Init;
Lapkepre; OutTextXY(180,10,'Kiválasztás'); Varj;
Kivalasztas;
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
7:If Kevert Then
Begin
Init; Lapkepre; OutTextXY(180,10,'Beszúrás'); Varj;
Beszuras;
OutTextXY(240,400,'Kész');
Varj; CloseGraph;
End;
8:If Kevert Then
Begin
Init;
Lapkepre; OutTextXY(180,10,'Jav.Beszúrás'); Varj;
JBeszuras;
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
9:If Kevert Then
Begin
Init;
Lapkepre; OutTextXY(180,10,'Quick'); Varj; Sz:= 0;
Quick(0, Db);
OutTextXY(240,400,'Kész'); Varj; CloseGraph;
End;
10:Begin Szinek(0,7); ClrScr; Halt End;
End;
Szinek(1,0); ClrScr;
ShowMouse;
Until False;
End.
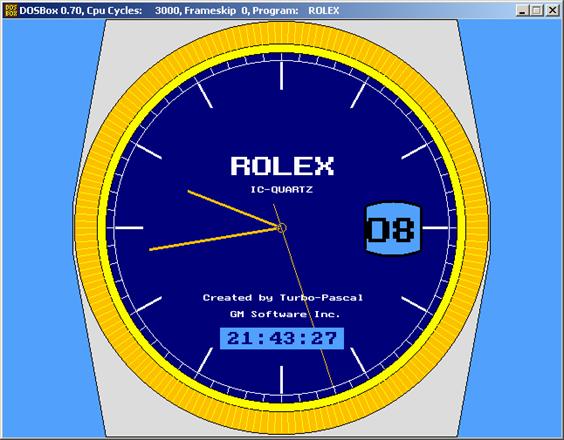
Írjunk grafikus analóg órát megjelenítő programot. Mutassa a másodperceket,
napokat, legyen digitális része is, és másodpercenként „ketyegő” hangot adjon.
Program
Rolex;
Uses
NewDelay, Crt, CrtPlus, Graph, Dos;
Type Datum= Record
Ev, Ho, Nap, NapNev: Word;
End;
Ido= Record
Ora, Perc, MPerc, SzMPerc: Word;
End;
Var RDatum,
UDatum: Datum;
RIdo, UIdo: Ido;
Ws, S: String;
Xm, Ym, Xk, Yk: Integer;
Var Start:
Boolean;
Procedure GrInit(Gi: Integer);
Var Gd, Gm:
Integer;
Begin
DetectGraph(Gd, Gm);
Gm:= Gi;
InitGraph(Gd,Gm,'C:\Tp\Bgi');
Xm:= GetMaxX; Ym:= GetMaxY; Xk:= Xm Div 2; Yk:= Ym Div 2;
End;
Procedure
Kep;
Var I:
Integer;
Begin
SetRGBPalette(0,20,40,63);
{Világoskék}
SetFillStyle(1,0);
Bar(0,0,Xm,Ym);
SetRGBPalette(1,0,0,0);
{Fekete}
SetColor(1);
SetLineStyle(0,0,2);
Circle(Xk,Yk,Yk-2);
Line(Xk - Yk,
Round(0.44*Ym),Xk - Yk, Round(0.56*Ym));
Line(Xk + Yk,
Round(0.44*Ym),Xk + Yk, Round(0.56*Ym));
Line(Xk - Round(0.42*Ym),
0, Xk - Yk, Round(0.44*Ym));
Line(Xk +
Round(0.42*Ym), 0, Xk + Yk, Round(0.44*Ym));
Line(Xk -
Round(0.42*Ym), Ym, Xk - Yk, Round(0.56*Ym));
Line(Xk +
Round(0.42*Ym), Ym, Xk + Yk, Round(0.56*Ym));
Line(Xk -
Round(0.42*Ym), 0, Xk + Round(0.42*Ym), 0);
Line(Xk -
Round(0.42*Ym), Ym, Xk + Round(0.42*Ym), Ym);
SetLineStyle(0,0,1);
Circle(Xk, Yk,
Round(0.44*Ym));
Circle(Xk, Yk,
Round(0.42*Ym));
SetRGBPalette(2,63,48,0); {Óarany}
SetColor(2);
SetFillStyle(1,2);
FloodFill(Xk - Round(0.45*Ym),
Yk, 1);
SetRGBPalette(3,63,63,0);
{Citromsárga}
SetColor(3);
SetFillStyle(1,3);
FloodFill(Xk -
Round(0.43*Ym), Yk, 1);
SetRGBPalette(4,0,0,30); {Sötétkék}
SetColor(4);
SetFillStyle(1,4);
FloodFill(Xk, Yk,
1);
SetRGBPalette(5,63,63,63); {Fehér}
SetColor(5);
Circle(Xk, Yk,
Round(0.4*Ym));
SetRGBPalette(7,55,55,55);
{Világosszürke}
SetColor(7);
SetFillStyle(1,7);
FloodFill(Xk -
Round(0.41*Ym), 3, 1);
SetColor(3);
SetLineStyle(0,0,1);
For
I:= 1 To 180 Do
Line(Xk +
Round(0.44*(Ym+2)*Cos(2*i*pi/180)),
Yk + Round(0.44*(Ym+2)*Sin(2*i*pi/180)),
Xk + Round(0.50*(Ym-8)*Cos(2*i*pi/180)),
Yk + Round(0.50*(Ym-8)*Sin(2*i*pi/180)));
SetColor(5);
SetLineStyle(0,0,1);
For
I:= 1 To 60 Do
Line(Xk +
Round(0.40*(Ym+3)*Cos(6*i*pi/180)),
Yk + Round(0.40*(Ym+3)*Sin(6*i*pi/180)),
Xk + Round(0.42*(Ym-3)*Cos(6*i*pi/180)),
Yk + Round(0.42*(Ym-3)*Sin(6*i*pi/180)));
SetLineStyle(0,0,3);
For
I:= 1 To 12 Do
Line(Xk +
Round(0.33*(Ym+3)*Cos(30*i*pi/180)),
Yk + Round(0.33*(Ym+3)*Sin(30*i*pi/180)),
Xk + Round(0.40*(Ym-3)*Cos(30*i*pi/180)),
Yk + Round(0.40*(Ym-3)*Sin(30*i*pi/180)));
SetColor(1);
SetLineStyle(0,0,3);
Line(Round(0.65*Xm),
Round(0.45*Ym), Round(0.65*Xm), Round(0.55*Ym));
Line(Round(0.75*Xm),
Round(0.45*Ym), Round(0.75*Xm), Round(0.55*Ym));
Ellipse(Round(0.7*Xm),Round(0.535*Ym),60,120,Round(0.1*Xm),Round(0.1*Ym));
Ellipse(Round(0.7*Xm),Round(0.465*Ym),240,300,Round(0.1*Xm),Round(0.1*Ym));
SetFillStyle(1,0);
FloodFill(Round(0.7*Xm),
Yk,1);
SetColor(5); {Szövegek}
SetTextStyle(0,0,3);
OutTextXY(Round(0.41*Xm),
Round(0.33*Ym), 'ROLEX');
SetTextStyle(0,0,1);
OutTextXY(Round(0.445*Xm),
Round(0.40*Ym), 'IC-QUARTZ');
OutTextXY(Round(0.36*Xm),
Round(0.66*Ym), 'Created by Turbo-Pascal');
OutTextXY(Round(0.408*Xm),
Round(0.70*Ym), 'GM Software Inc.');
SetLineStyle(0,0,1);
SetColor(2); Circle(Xk, Yk, Round(0.01*Ym));
{Nap}
SetColor(1);
Str(UDatum.Nap,ws);
If
Length(Ws)=1 Then
Ws:='0'+Ws;
SetTextStyle(0,0,4);
OutTextXY(Round(0.65*Xm),Round(0.475*Ym), Ws);
End;
Procedure
Ora;
Begin
RDatum:=UDatum; With UDatum Do GetDate(Ev, Ho, Nap, NapNev);
RIdo:=UIdo; With UIdo Do GetTime(Ora, Perc, MPerc, SzMPerc);
If
UIdo.MPerc<>RIdo.MPerc Then With UIdo Do
Begin
SetColor(6);
If
Not Start Then {Analóg}
With
RIdo Do
Begin
SetLineStyle(0,0,1);
Line(Xk -
Round(0.06*Ym*Sin(MPerc*6*Pi/180)),
Yk + Round(0.06*Ym*Cos(MPerc*6*Pi/180)),
Xk + Round(0.40*Ym*Sin(MPerc*6*Pi/180)),
Yk - Round(0.40*Ym*Cos(MPerc*6*Pi/180)));
SetLineStyle(0,0,3);
Line(Xk, Yk, Xk
+ Round(0.32*Ym*Sin((Perc*6+MPerc/10)*Pi/180)),
Yk - Round(0.32*Ym*Cos((Perc*6+MPerc/10)*Pi/180)));
SetLineStyle(0,0,3);
Line(Xk, Yk, Xk
+ Round(0.24*Ym*Sin((Ora*30+Perc/2)*Pi/180)),
Yk - Round(0.24*Ym*Cos((Ora*30+Perc/2)*Pi/180)));
End
Else
Start:= False;
With
UIdo Do
Begin
SetLineStyle(0,0,1);
Line(Xk -
Round(0.06*Ym*Sin(MPerc*6*Pi/180)),
Yk + Round(0.06*Ym*Cos(MPerc*6*Pi/180)),
Xk + Round(0.40*Ym*Sin(MPerc*6*Pi/180)),
Yk - Round(0.40*Ym*Cos(MPerc*6*Pi/180)));
SetLineStyle(0,0,3);
Line(Xk ,Yk, Xk
+ Round(0.32*Ym*Sin((Perc*6+MPerc/10)*Pi/180)),
Yk - Round(0.32*Ym*Cos((Perc*6+MPerc/10)*Pi/180)));
SetLineStyle(0,0,3);
Line(Xk, Yk, Xk
+ Round(0.24*Ym*Sin((Ora*30+Perc/2)*Pi/180)),
Yk - Round(0.24*Ym*Cos((Ora*30+Perc/2)*Pi/180)));
SetFillStyle(0,1);
Bar(Round(0.66*Xm),
Round(0.474*Ym),
Round(0.73*Xm),
Round(0.52*Ym));
SetColor(1);
Str(UDatum.Nap,ws);
If
Length(Ws)=1 Then
Ws:='0'+Ws;
SetTextStyle(0,0,4);
OutTextXY(Round(0.65*Xm),Round(0.475*Ym),
Ws);
End;
{Digitális}
S:=''; Str(Ora,
Ws); If Ora<10 Then Ws:='0'+Ws; S:=Ws+':';
Str(Perc, Ws); If Perc<10 Then Ws:='0'+Ws; S:=S+WS+':';
Str(MPerc, WS); If MPerc<10 Then Ws:='0'+Ws; S:=S+WS;
SetColor(0);
Bar(Round(0.39*Xm),
Round(0.74*Ym), Round(0.61*Xm), Round(0.79*Ym));
Setcolor(4);
SetTextStyle(0,0,2);
OutTextXY(Round(0.403*Xm),Round(0.75*Ym),
S);
SetColor(6);
Sound(6000);delay(5);Nosound;
End;
End;
Begin
With
UDatum Do GetDate(Ev,
Ho, Nap, NapNev);
With
UIdo Do GetTime(Ora,
Perc, MPerc, SzMPerc);
GrInit(2);
Kep; SetWriteMode(XORPut);Start:=
True;
Repeat
Ora Until Keypressed;
End.
Sztereó
Ezen a lapon a térnek síkban
(képernyőn) történő ábrázolására mutatunk néhány programot. Az alapja a
projekció, azaz testek megatározó pontjainak a síkra történő vetítése. Minden
programban valamilyen egyszerű test, térbeli mozgást végez.
A projekció mellett a tér érzékeltetését kétféle módon
oldjuk majd meg. Az első esetben a test nem átlátszó, a térbeliséget a
láthatósággal valósítjuk meg, így miközben az ábrázolás egyszerű projekció,
ennek ellenére szemünk hajlandó térbeliséget kölcsönözni a látványnak.
Második esetben a testek átlátszók, úgynevezett
dróthálós megjelenítésűek, viszont kettős projekciót hajtunk végre, külön-külön
a két szem számára, ezeket a vetületeket különböző
színekkel fogjuk megrajzolni és a sztereóhatást színes (térhatású képek, filmek
nézésére alkalmas kétszínű) szemüveggel fogjuk elérni.
Először nézzük az egy centrumú
projekciót. Ennek szemléltetésére egy rajzot nézhetünk meg, mely Turbo
Pascal-ban készült, grafikus képernyőre:
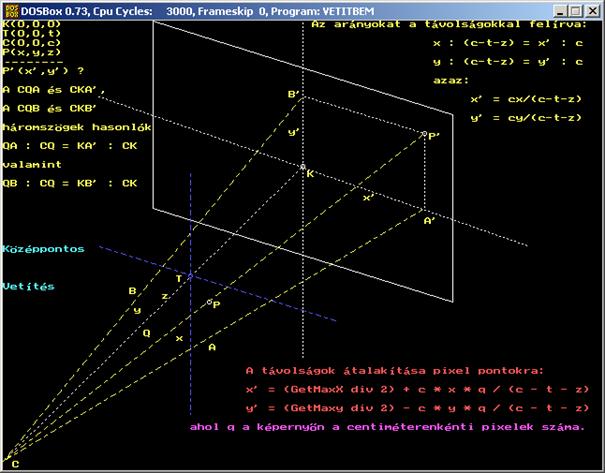
Másodjára a két középpontú (a két
szemnek megfelelő távolságú) projekciót tekinthetjük meg egy, az előzőhöz
hasonló ábrán.
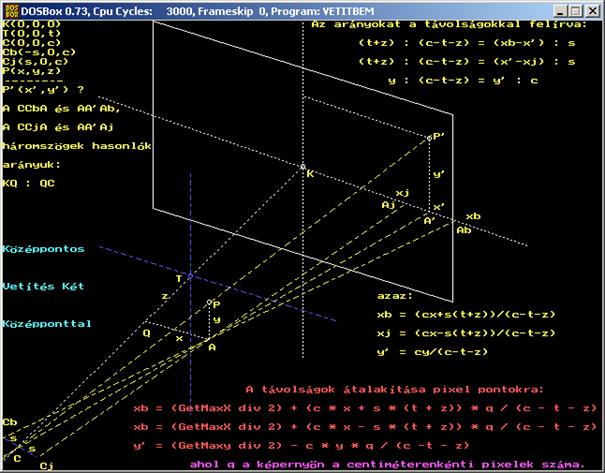
Az előző ábrákon található, a
vetítéseket létrehozó összefüggések a programjainkban megtalálhatóak.
Szükségünk van még a mozgáshoz a vektorok térbeli transzformációs mátrixára,
valamint a konvex testek felületének láthatóságát meghatározó vektoriális
szorzatra. A programokban előforduló testek: 9 alapélű kettős gúla (egy
csiszolt gyémánthoz hasonló, némi jóindulattal), az öt szabályos test
(tetraéder, kocka, oktaéder, ikozaéder, dodekaéder), valamint az egyköpenyű
hiperboloid és a hiperbolikus paraboloid.
Nézzünk az első lehetőségre egy
programot. Egy futtatási képe:
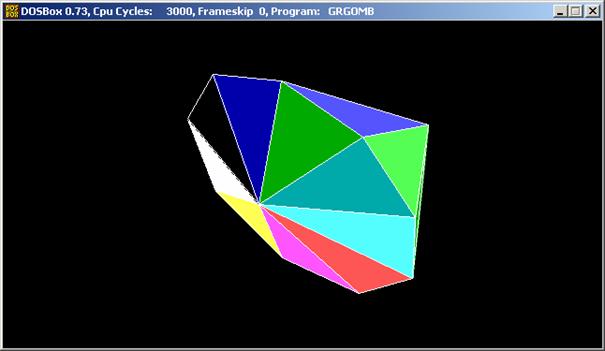
Ennek a programnak a listája:
Program GrGula;
Uses NewDelay,Crt, Graph;
Const c = 260;
t = 50;
a = 10;
qx = 15;
qy = 11;
n = 9;
Cs = n+2;
Lc = 3;
Ls = 2*n;
Type Vekt = Array[1..3] Of Real;
Csucsok= Array[1..Cs] Of Vekt;
Lapok = Array[1..Ls,1..Lc] Of Byte;
Const Al : Integer= 2;
Be : Integer= 0;
Ga : Integer= 1;
Var Mx, My: Integer;
Kx, Ky: Integer;
Page : Word;
Test: Csucsok;
TestL: Lapok;
S: Longint;
Procedure GrInit;
Var Gd, Gm: Integer;
Begin
DetectGraph(Gd, Gm); Gm:=
1; InitGraph(Gd, Gm, 'c:\Tp\Bgi');
Mx:= GetMaxX; Kx:= Mx Div 2; My:= GetMaxY; Ky:= My Div 2;
End;
Procedure Gula;
Var i: Byte;
Begin
Test[1,1]:=0; Test[1,2]:=0; Test[1,3]:=a;
For i:=0 to n-1 do
Begin
Test[i+2,1]:=a*Cos(i*360/n*Pi/180);
Test[i+2,2]:=a*Sin(i*360/n*Pi/180);
Test[i+2,3]:=0;
End;
Test[n+2,1]:=0; Test[n+2,2]:=0; Test[n+2,3]:=-a/3;
For i:=1 to n-1 Do
Begin
TestL[i,1]:=1;
TestL[i,2]:=i+1;
TestL[i,3]:=i+2;
End;
TestL[n,1]:=1; TestL[n,2]:=n+1; TestL[n,3]:=2;
For i:=n+1 to 2*n-1 Do
Begin
TestL[i,1]:=n+2;
TestL[i,2]:=i-n+2;
TestL[i,3]:=i-n+1;
End;
TestL[2*n,1]:=n+2; TestL[2*n,2]:=2; TestL[2*n,3]:=n+1;
End;
Procedure Forgatas;
Var i: Byte;
Px, Py, Pz: Real;
SinAl, CosAl, SinBe, CosBe, SinGa, CosGa: Real;
Begin
Inc(S); If S Mod 100=0 Then
Begin
Al:= Al+Random(2)-1;
Be:= Be+Random(2)-1;
Ga:= Ga+Random(2)-1;
If Abs(Al)>4 Then Al:= 2;
If Abs(Be)>2 Then Be:= 0;
If Abs(Ga)>3 Then Ga:= 1;
End;
SinAl:= Sin(Al*pi/180); CosAl:= Cos(Al*pi/180);
SinBe:= Sin(Be*pi/180); CosBe:= Cos(Be*pi/180);
SinGa:= Sin(Ga*pi/180); CosGa:= Cos(Ga*pi/180);
For i:= 1 To Cs Do
Begin
Px:= Test[i,1]*CosBe*CosGa-
Test[i,2]*CosBe*SinGa+Test[i,3]*SinBe;
Py:= Test[i,1]*(CosAl*SinGa+SinAl*SinBe*CosGa)+
Test[i,2]*(CosAl*CosGa-SinAl*SinBe*SinGa)-
Test[i,3]*SinAl*CosBe;
Pz:= Test[i,1]*(SinAl*SinGa-CosAl*SinBe*CosGa)+
Test[i,2]*(SinAl*CosGa+CosAl*SinBe*SinGa)+
Test[i,3]*CosAl*CosBe;
Test[i,1]:= Px;
Test[i,2]:= Py;
Test[i,3]:= Pz;
End;
End;
Procedure Vetites;
Var Kp: Array[1..Lc+1] Of PointType;
i, j: Byte;
s, k1, k2: Vekt;
CosDe: Real;
Procedure VektSzor(a, b: Vekt; Var s: Vekt);
Begin
s[1]:= a[2]*b[3]-a[3]*b[2];
s[2]:= a[3]*b[1]-a[1]*b[3];
s[3]:= a[1]*b[2]-a[2]*b[1];
End;
Procedure VektKul(a, b: Vekt; Var k: Vekt);
Begin
k[1]:= a[1]-b[1];
k[2]:= a[2]-b[2];
k[3]:= a[3]-b[3];
End;
Begin
SetActivePage(Page);
ClearDevice;
For I:= 1 To Ls Do
Begin
For J:= 1 To Lc Do
Begin
If j = 1 Then
Begin
Kp[Lc+1].x:= Round(Kx + c * Test[TestL[i,j],1] * qx/
(c - t - Test[TestL[i,j],3]));
Kp[Lc+1].y:= Round(Ky - c * Test[TestL[i,j],2] * qy/
(c - t - Test[TestL[i,j],3]));
End;
Kp[j].x:= Round(Kx + c * Test[TestL[i,j],1] * qx/
(c - t - Test[TestL[i,j],3]));
Kp[j].y:= Round(Ky - c * Test[TestL[i,j],2] * qy/
(c - t - Test[TestL[i,j],3]));
End;
If Kp[1].x*(Kp[2].y-Kp[3].y)+
Kp[2].x*(Kp[3].y-Kp[1].y)+
Kp[3].x*(Kp[1].y-Kp[2].y)<0 Then
Begin
SetFillStyle(1,i+1);
FillPoly(3, Kp);
End;
End;
SetVisualPage(Page);
Page:=1-Page;
End;
Var p: array[1..Lc] of PointType;
Begin
GrInit;
Delay(1500);
Gula;
Page:=0;
Repeat
Vetites;
Forgatas;
While ((Port[$3DA] And 8) <> 8) Do;
Until KeyPressed;
End.
Térjünk át a második lehetőségre. A kétszínű
megjelenítéshez szükség van egy segédprogramra, mert a megfelelő hatás elérése
érdekében, a két képernyő színt és a szemüveg két színét össze kell illeszteni.
Erre lesz alkalmas a Színválasztó program. A szemüveget a képernyőre kell
helyezni, az alatta elhelyezkedő, vele azonos színű vonalat nem szabad látni,
az ellentétes színű vonalat pedig feketének (ez jelenti az összehangolást, majd
a beállítás RGB értékeit be kell írni a SetRGBPalette
eljárás hívásába, paraméterekként).

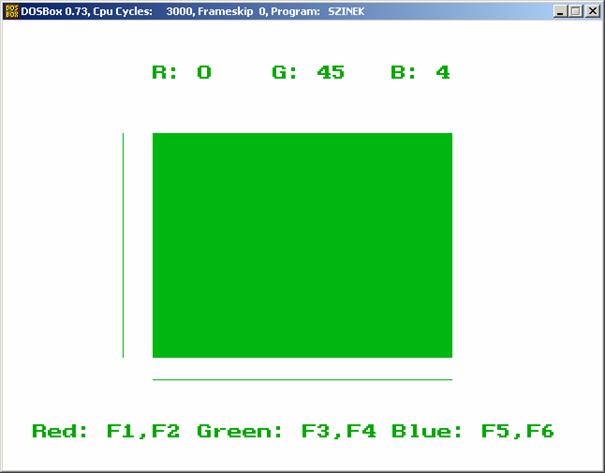
A színeket beállító program listája:
Program Szinek;
Uses NewDelay, Crt, CrtPlus, Graph;
Var Mx, My:Integer;
R, G, B: Byte;
Ch: Char;
S: String;
Procedure GrInit;
Var Gd, Gm: Integer;
Begin
DetectGraph(Gd,Gm);
InitGraph(Gd,Gm,'C:\Tp\Bgi');
End;
Begin
GrInit; Mx:= GetMaxX; My:= GetMaxY;
SetRGBPalette(0,63,63,63);
SetFillStyle(1,0);
Bar(0,0,Mx,My);
SetTextStyle(0,0,2);
SetColor(2);
MoveTo(Round(0.05*Mx),Round(0.9*My));
OutText('Red: F1,F2 Green: F3,F4 Blue: F5,F6');
Repeat
SetFillStyle(1,0);
Bar(Round(0.2*Mx),Round(0.1*My),
Round(0.8*Mx),Round(0.2*My));
SetColor(2);
MoveTo(Round(0.25*Mx),Round(0.1*My));
Str(R,S); OutText('R: '+S);
MoveTo(Round(0.45*Mx),Round(0.1*My));
Str(G,S); OutText('G: '+S);
MoveTo(Round(0.65*Mx),Round(0.1*My));
Str(B,S); OutText('B: '+S);
SetRGBPalette(1,R,G,B);
SetColor(1);
SetFillStyle(1,1);
Bar(Round(0.25*Mx),Round(0.25*My),
Round(0.75*Mx),Round(0.75*My));
Line(Round(0.2*Mx),Round(0.25*My),
Round(0.2*Mx),Round(0.75*My));
Line(Round(0.25*Mx),Round(0.8*My),
Round(0.75*Mx),Round(0.8*My));
Ch:= ReadKey;
If Ch = #0 Then
Begin
Ch:= ReadKey;
Case Ch Of
#59: If R>0 Then Dec(R);
#60: If R<63 Then Inc(R);
#61: If G>0 Then Dec(G);
#62: If G<63 Then Inc(G);
#63: If B>0 Then Dec(B);
#64: If B<63 Then Inc(B);
End;
End;
Until Ch= #27;
CloseGraph;
End.
Nyilvánvaló, hogy az IMAX által kínált 3D-s filmek, és
a nemrég megjelent Avatar korában az így vázolt látvány igen szerény, de a
dróthálós, kétszínű megjelenítésben a lényeg benne van (külön készül rajz a két
szemnek, és agyunkban összeáll térhatású képpé), és csak ezt szeretné
bemutatni, ez az egyszerű program.
Néhány futási képet nézzünk meg a
dróthálós megjelenítésű programból. A
menü:
Az oktaéder:

Az ikozaéder:
Az egyköpenyű hiperboloid:
A program egy, a geometriai elemeket tartalmazó UST nevű
Unit-ot használ. Ennek és a programnak a listája:
Unit UST;
Interface
Uses
Graph;
Const
KS= 25;
KM= 18;
KT= 100;
ST= 3.5;
HSzin= 7;
JSzin= 3;
BSzin= 4;
Type
Vektor= Array[1..3] Of Real;
Var
Kx, Ky: Integer;
H, S : Vektor;
A, B : Vektor;
DX, DY, DZ: Real;
DAl, DBe, DGa: Real;
I : Integer;
N : Integer;
Procedure Forgato(Var Z:Vektor;U,F:Vektor);
Procedure LinKep(Var H, S: Vektor; V, W: Vektor; JSzin, Bszin: Byte);
Procedure Init;
Implementation
Procedure Forgato(Var Z:Vektor;U,F:Vektor);
Begin
Z[1]:=U[1]*Cos(F[2])*Cos(F[3])-U[2]*Cos(F[2])*Sin(F[3])+U[3]*Sin(F[2]);
Z[2]:=U[1]*(Cos(F[1])*Sin(F[3])+Sin(F[1])*Sin(F[2])*Cos(F[3]))
+U[2]*(Cos(F[1])*Cos(F[3])-Sin(F[1])*Sin(F[2])*Sin(F[3]))
-U[3]*Sin(F[1])*Cos(F[2]);
Z[3]:=U[1]*(Sin(F[1])*Sin(F[3])-Cos(F[1])*Sin(F[2])*Cos(F[3]))
+U[2]*(Sin(F[1])*Cos(F[3])+Cos(F[1])*Sin(F[2])*Sin(F[3]))
+U[3]*Cos(F[1])*Cos(F[2]);
end;
Procedure LinKep(Var H, S: Vektor; V, W: Vektor; JSzin, Bszin: Byte);
Var VJX, VJY, VBX, VBY, WJX, WJY, WBX, WBY: Integer;
Begin
Forgato(V,V,S);
Forgato(W,W,S);
VJX:=Round((KT*(KS+V[1]+H[1])+(V[3]+H[3])*(KS-ST))/(KT+V[3]+H[3])*Kx/Ks);
VJY:=Round((KT*(KM-V[2]-H[2])+(V[3]+H[3])*KM)/(KT+V[3]+H[3])*KY/KM);
VBX:=Round((KT*(KS+V[1]+H[1])+(V[3]+H[3])*(KS+ST))/(KT+V[3]+H[3])*Kx/Ks);
VBY:=Round((KT*(KM-V[2]-H[2])+(V[3]+H[3])*KM)/(KT+V[3]+H[3])*KY/KM);
WJX:=Round((KT*(KS+W[1]+H[1])+(W[3]+H[3])*(KS-ST))/(KT+W[3]+H[3])*Kx/Ks);
WJY:=Round((KT*(KM-W[2]-H[2])+(W[3]+H[3])*KM)/(KT+W[3]+H[3])*KY/KM);
WBX:=Round((KT*(KS+W[1]+H[1])+(W[3]+H[3])*(KS+ST))/(KT+W[3]+H[3])*Kx/Ks);
WBY:=Round((KT*(KM-W[2]-H[2])+(W[3]+H[3])*KM)/(KT+W[3]+H[3])*KY/KM);
SetColor(JSzin); Line(VJX,VJY,WJX,WJY);
SetColor(BSzin); Line(VBX,VBY,WBX,WBY);
End;
Procedure Init;
Var Gd, Gm: Integer;
Begin
DetectGraph(Gd, Gm); InitGraph(Gd, Gm, 'C:\Tp\Bin');
Kx:= Round(GetMaxX/2);
Ky:= Round(GetMaxY/2);
SetColor(JSzin);
SetRGBPalette(JSzin, 0, 45, 4);
SetColor(BSzin);
SetRGBPalette(BSzin, 47, 13, 0);
SetBkColor(HSzin);
ClearDevice;
End;
End.
A program listája:
Program StOk;
Uses NewDelay, Crt, CrtPlus, Graph, UST;
Const MaxI= 200;
MPont:Array[1..8] Of String[25]=
(' Tetraéder ',
' Kocka ',
' Oktaéder ',
' Dodekaéder ',
' Ikozaéder ',
' Egyköpenyű hiperboloid ',
' Hiperbolikus paraboloid ',
' Kilépés a programból ');
Var AT, BT: Array[1..MaxI] Of Vektor;
MP: Byte;
Procedure Kezdet;
Begin
H[1]:= 0; H[2]:= 0; H[3]:= -40;
S[1]:= 0; S[2]:= 0; S[3]:= 0;
DX:= 0.07; DY:= 0.05; DZ:=0.03;
DAl:= 0.05; DBe:= 0.03; DGa:= 0.02;
End;
Procedure Mozgas;
Begin
H[1]:= H[1]+DX; If (H[1]<-8) Or (H[1]>8) Then DX:=-DX;
H[2]:= H[2]+DY; If (H[2]<-8) Or (H[2]>8) Then DY:=-DY;
H[3]:= H[3]+DZ; If (H[3]<-50) Or (H[3]>-10) Then DZ:=-DZ;
S[1]:= S[1]+DAl;
S[2]:= S[2]+DBe;
S[3]:= S[3]+DGa;
End;
Procedure EgykopenyuHip;
Var P : Real;
Ra, Rf: Real;
Ma, Mf: Real;
Ds, IM: Integer;
Begin
Ra:= 4; Rf:= 2;
Ma:= -3; Mf:= 3;
P:= 2;
Ds:=20; IM:= 19;
N:=0;
For I:=1 To IM Do
Begin
A[1]:=Rf*Cos(I*Ds*Pi/180+P);
A[2]:=Mf;
A[3]:=Rf*Sin(I*Ds*Pi/180+P);
B[1]:=Ra*Cos(I*Ds*Pi/180);
B[2]:=Ma;
B[3]:=Ra*Sin(I*Ds*Pi/180);
Inc(N); AT[N]:=A; BT[N]:=B;
B[1]:=Rf*Cos((I+1)*Ds*Pi/180+P);
B[2]:=Mf;
B[3]:=Rf*Sin((I+1)*Ds*Pi/180+P);
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Ra*Cos(I*Ds*Pi/180);
A[2]:=Ma;
A[3]:=Ra*Sin(I*Ds*Pi/180);
B[1]:=Ra*Cos((I+1)*Ds*Pi/180);
B[2]:=Ma;
B[3]:=Ra*Sin((I+1)*Ds*Pi/180);
Inc(N); AT[N]:=A; BT[N]:=B;
End;
End;
Procedure HipPar;
Begin
N:=0;
For I:=0 To 15 Do
Begin
A[1]:=-6; A[2]:=0; A[3]:=6-I*0.8;
B[1]:= 6; B[2]:=6-I*0.8; B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
A[1]:=-6; A[2]:=0; A[3]:=6;
B[1]:=-6; B[2]:=0; B[3]:=6-I*0.8;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:= 6; A[2]:=6; A[3]:=0;
B[1]:= 6; B[2]:=6-I*0.8; B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
Procedure Oktaeder;
Const E=5;
Begin
N:=0;
A[1]:=E;A[2]:=0;A[3]:=0;
B[1]:=0;B[2]:=E;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=E;A[3]:=0;
B[1]:=-E;B[2]:=0;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=0;A[3]:=0;
B[1]:=0;B[2]:=-E;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-E;A[3]:=0;
B[1]:=E;B[2]:=0;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=0;A[3]:=E;
B[1]:=0;B[2]:=E;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=E;A[3]:=0;
B[1]:=0;B[2]:=0;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=0;A[3]:=-E;
B[1]:=0;B[2]:=-E;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-E;A[3]:=0;
B[1]:=0;B[2]:=0;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=0;A[3]:=0;
B[1]:=0;B[2]:=0;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=0;A[3]:=-E;
B[1]:=-E;B[2]:=0;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=0;A[3]:=0;
B[1]:=0;B[2]:=0;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=0;A[3]:=E;
B[1]:=E;B[2]:=0;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
Procedure Kocka;
Const E=3;
Begin
n:=0;
A[1]:=E;A[2]:=E;A[3]:=E;
B[1]:=-E;B[2]:=E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=E;A[3]:=E;
B[1]:=-E;B[2]:=E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=E;A[3]:=-E;
B[1]:=E;B[2]:=E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=E;A[3]:=-E;
B[1]:=E;B[2]:=E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=-E;A[3]:=E;
B[1]:=-E;B[2]:=-E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=-E;A[3]:=E;
B[1]:=-E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=-E;A[3]:=-E;
B[1]:=E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=-E;A[3]:=-E;
B[1]:=E;B[2]:=-E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=E;A[3]:=E;
B[1]:=E;B[2]:=-E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=E;A[3]:=E;
B[1]:=-E;B[2]:=-E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=E;A[3]:=-E;
B[1]:=-E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=E;A[3]:=-E;
B[1]:=E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
Procedure Tetraeder;
Const E=3;
Begin
N:=0;
A[1]:=E;A[2]:=E;A[3]:=E;
B[1]:=-E;B[2]:=E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=-E;A[3]:=E;
B[1]:=E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=E;A[3]:=E;
B[1]:=-E;B[2]:=-E;B[3]:=E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=E;A[2]:=E;A[3]:=E;
B[1]:=E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=-E;A[3]:=E;
B[1]:=-E;B[2]:=E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-E;A[2]:=E;A[3]:=-E;
B[1]:=E;B[2]:=-E;B[3]:=-E;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
Procedure Ikozaeder;
Const E=6;
Var R, X, Y, V, Z, U, T: Real;
Begin
R:= E*SQRT(2*(5+SQRT(5)))/4;
X:= E*SQRT((5+SQRT(5))/10);
Y:= E*SQRT((5-SQRT(5))/10);
Z:= E*SQRT((5+2*SQRT(5))/20);
U:= E*SQRT(1/(10+2*SQRT(5)));
V:= E*SQRT((5+2*SQRT(5))/(10+2*SQRT(5)));
T:= R-Y;
N:=0;
A[1]:=X;A[2]:=T;A[3]:=0;
B[1]:=U;B[2]:=T;B[3]:=V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U;A[2]:=T;A[3]:=V;
B[1]:=-Z;B[2]:=T;B[3]:=E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z;A[2]:=T;A[3]:=E/2;
B[1]:=-Z;B[2]:=T;B[3]:=-E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z;A[2]:=T;A[3]:=-E/2;
B[1]:=U;B[2]:=T;B[3]:=-V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U;A[2]:=T;A[3]:=-V;
B[1]:=X;B[2]:=T;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=R;A[3]:=0;
B[1]:=X;B[2]:=T;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=R;A[3]:=0;
B[1]:=U;B[2]:=T;B[3]:=V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=R;A[3]:=0;
B[1]:=-Z;B[2]:=T;B[3]:=E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=R;A[3]:=0;
B[1]:=-Z;B[2]:=T;B[3]:=-E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=R;A[3]:=0;
B[1]:=U;B[2]:=T;B[3]:=-V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-X;A[2]:=-T;A[3]:=0;
B[1]:=-U;B[2]:=-T;B[3]:=V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U;A[2]:=-T;A[3]:=V;
B[1]:=Z;B[2]:=-T;B[3]:=E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Z;A[2]:=-T;A[3]:=E/2;
B[1]:=Z;B[2]:=-T;B[3]:=-E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Z;A[2]:=-T;A[3]:=-E/2;
B[1]:=-U;B[2]:=-T;B[3]:=-V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U;A[2]:=-T;A[3]:=-V;
B[1]:=-X;B[2]:=-T;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-R;A[3]:=0;
B[1]:=-X;B[2]:=-T;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-R;A[3]:=0;
B[1]:=-U;B[2]:=-T;B[3]:=V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-R;A[3]:=0;
B[1]:=Z;B[2]:=-T;B[3]:=E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-R;A[3]:=0;
B[1]:=Z;B[2]:=-T;B[3]:=-E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=0;A[2]:=-R;A[3]:=0;
B[1]:=-U;B[2]:=-T;B[3]:=-V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=X;A[2]:=T;A[3]:=0;
B[1]:=Z;B[2]:=-T;B[3]:=-E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=X;A[2]:=T;A[3]:=0;
B[1]:=Z;B[2]:=-T;B[3]:=E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U;A[2]:=T;A[3]:=V;
B[1]:=Z;B[2]:=-T;B[3]:=E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U;A[2]:=T;A[3]:=V;
B[1]:=-U;B[2]:=-T;B[3]:=V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z;A[2]:=T;A[3]:=E/2;
B[1]:=-U;B[2]:=-T;B[3]:=V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z;A[2]:=T;A[3]:=E/2;
B[1]:=-X;B[2]:=-T;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z;A[2]:=T;A[3]:=-E/2;
B[1]:=-X;B[2]:=-T;B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z;A[2]:=T;A[3]:=-E/2;
B[1]:=-U;B[2]:=-T;B[3]:=-V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U;A[2]:=T;A[3]:=-V;
B[1]:=-U;B[2]:=-T;B[3]:=-V;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U;A[2]:=T;A[3]:=-V;
B[1]:=Z;B[2]:=-T;B[3]:=-E/2;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
Procedure Dodekaeder;
Const E=3;
Var X, Y, Z, U, U1, U2, V, V1, V2, R, R1, R2, P, Q: Real;
Begin
X:= E*SQRT((5+SQRT(5))/10);
Z:=E*SQRT((5+2*SQRT(5))/20);
R:= E/2*SQRT((25+11*SQRT(5))/10);
R1:= R*(3-SQRT(5));
R2:= R*(SQRT(5)-1);
Y:= R*(SQRT(5)-2);
P:= SQRT(E*E-R1*R1);
Q:= SQRT((X+Z)*(X+Z)-R2*R2);
U:= E*SQRT(1/(10+2*SQRT(5)));
U1:= U*(X+P)/X;
U2:= Z*(X+P)/X;
V:= E*SQRT((5+2*SQRT(5))/(10+2*SQRT(5)));
V1:= V*(X+P)/X;
V2:= E*(P+X)/2/X;
N:=0;
A[1]:=0;A[2]:=0;A[3]:=0;B[1]:=0;B[2]:=0;B[3]:=0;Inc(N);AT[N]:=A;BT[N]:=B;
A[1]:=X;A[2]:=R;A[3]:=0;B[1]:=U;B[2]:=R;B[3]:=V;Inc(N);AT[N]:=A;BT[N]:=B;
A[1]:=U;A[2]:=R;A[3]:=V;B[1]:=-Z;B[2]:=R;B[3]:=E/2;Inc(N);AT[N]:=A;BT[N]:=B;
A[1]:=-Z;A[2]:=R;A[3]:=E/2;B[1]:=-Z;B[2]:=R;B[3]:=-E/2;Inc(N);AT[N]:=A;BT[N]:=B;
A[1]:=-Z;A[2]:=R;A[3]:=-E/2;B[1]:=U;B[2]:=R;B[3]:=-V;Inc(N);AT[N]:=A;BT[N]:=B;
A[1]:=U;A[2]:=R;A[3]:=-V;B[1]:=X;B[2]:=R;B[3]:=0;Inc(N);AT[N]:=A;BT[N]:=B;
A[1]:=X; A[2]:=R; A[3]:=0;
B[1]:=X+P; B[2]:=Y; B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U; A[2]:=R; A[3]:=V;
B[1]:=U1; B[2]:=Y; B[3]:=V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z; A[2]:=R; A[3]:=E/2;
B[1]:=-U2; B[2]:=Y; B[3]:=V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-Z; A[2]:=R; A[3]:=-E/2;
B[1]:=-U2; B[2]:=Y; B[3]:=-V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U; A[2]:=R; A[3]:=-V;
B[1]:=U1; B[2]:=Y; B[3]:=-V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Z; A[2]:=-R; A[3]:=-E/2;B[1]:=Z; B[2]:=-R; B[3]:=E/2;Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Z; A[2]:=-R; A[3]:=E/2;B[1]:=-U; B[2]:=-R; B[3]:=V;Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U; A[2]:=-R; A[3]:=V;B[1]:=-X; B[2]:=-R; B[3]:=0;Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-X; A[2]:=-R; A[3]:=0;B[1]:=-U; B[2]:=-R; B[3]:=-V;Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U; A[2]:=-R; A[3]:=-V;B[1]:=Z; B[2]:=-R; B[3]:=-E/2;Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Z; A[2]:=-R; A[3]:=-E/2;
B[1]:=U2; B[2]:=-Y; B[3]:=-V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=Z; A[2]:=-R; A[3]:=E/2;
B[1]:=U2; B[2]:=-Y; B[3]:=V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U; A[2]:=-R; A[3]:=V;
B[1]:=-U1; B[2]:=-Y; B[3]:=V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-X; A[2]:=-R; A[3]:=0;
B[1]:=-X-P; B[2]:=-Y; B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U; A[2]:=-R; A[3]:=-V;
B[1]:=-U1; B[2]:=-Y; B[3]:=-V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=X+P; A[2]:=Y; A[3]:=0;
B[1]:=U2; B[2]:=-Y; B[3]:=-V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=X+P; A[2]:=Y; A[3]:=0;
B[1]:=U2; B[2]:=-Y; B[3]:=V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U1; A[2]:=Y; A[3]:=V1;
B[1]:=U2; B[2]:=-Y; B[3]:=V2;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U1; A[2]:=Y; A[3]:=V1;
B[1]:=-U1; B[2]:=-Y; B[3]:=V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U2; A[2]:=Y; A[3]:=V2;
B[1]:=-U1; B[2]:=-Y; B[3]:=V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U2; A[2]:=Y; A[3]:=V2;
B[1]:=-X-P; B[2]:=-Y; B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U2; A[2]:=Y; A[3]:=-V2;
B[1]:=-X-P; B[2]:=-Y; B[3]:=0;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=-U2; A[2]:=Y; A[3]:=-V2;
B[1]:=-U1; B[2]:=-Y; B[3]:=-V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U1; A[2]:=Y; A[3]:=-V1;
B[1]:=-U1; B[2]:=-Y; B[3]:=-V1;
Inc(N); AT[N]:=A; BT[N]:=B;
A[1]:=U1; A[2]:=Y; A[3]:=-V1;
B[1]:=U2; B[2]:=-Y; B[3]:=-V2;
Inc(N); AT[N]:=A; BT[N]:=B;
End;
Begin
MP:=1;
Repeat
Szinek(1,14);
ClrScr;
Ablak(7,0,24,4,52,13,true,'Menü');
For I:=1 To 8 Do WriteXY(26,4+I,MPont[i]);
MP:=Menu(7,0,2,26,5,25,8,MP);
Case Mp Of
1:Tetraeder;
2:Kocka;
3:Oktaeder;
4:Dodekaeder;
5:Ikozaeder;
6:EgykopenyuHip;
7:HipPar;
8:Halt;
End;
Init;Kezdet;
Repeat
Mozgas;
For I:=1 To N Do LinKep(H,S,AT[I],BT[I],JSzin,BSzin);
Delay(100);
ClearDevice;
Until KeyPressed;
CloseGraph;
While keypressed do readkey;
If MP=0 Then MP:=1;
Until False;
End.
Írjunk programot, mely a Naprendszert
szemlélteti. A bolygók együttállásból (északról) induljanak, pályájuk legyen
ellipszis, a Naptól mért távolságoknak nem kell a valósággal arányosnak lenni.
A bolygók mérete némileg tükrözze a nagysági viszonyúkat, relatív keringési
idejük viszont a valóságot jól tükrözze. A bolygók különböző színűek legyenek,
egyezzen meg a pályájuk színével. A Föld kék, a Mars vörös legyen. A Nap és a
Jupiter sárga.
Egy lehetséges megvalósítás futási képe:
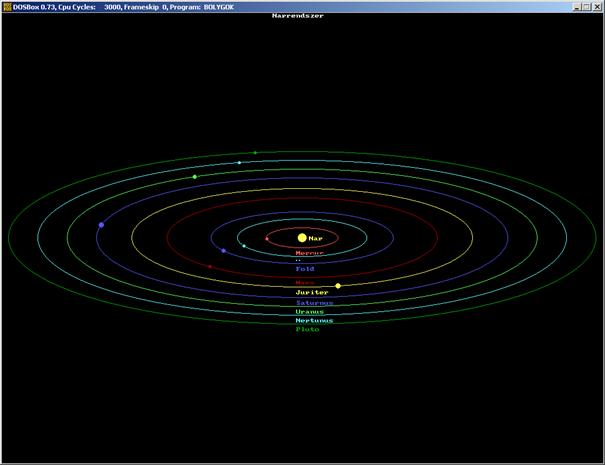
A program listája:
Program Bolygok;
Uses NewDelay, Crt, CrtPlus,
Graph;
Const A:
Real= 0.3;
Uc: Byte= 0;
Var Xk, Yk: Integer;
Type TBolygo= Object
FRn, FRk, FKi, Fr: LongInt;
FFi: Real;
FC: Byte;
Procedure
Init(IRn, IRk, IKi, Ir: LongInt; IFi: Real; IC: Byte);
Function
GetKis: Integer;
Function GetNagy: Integer;
Procedure
Hely;
Procedure
Show;
Procedure
Hide;
Procedure
Mozgas;
Private
Fx, Fy: Integer;
End;
TControl= Object
Nap, Mercur, Venus, Fold, Mars, Jupiter,
Saturnus, Uranus, Neptunus, Pluto:
TBolygo;
Procedure
Init;
Procedure
Run;
Procedure
Done;
End;
Procedure TBolygo.Init(IRn,
IRk, IKi, Ir: LongInt; IFi: Real; IC: Byte);
Begin
FRn:= IRn; {Nagy sugár}
FRk:= IRk; {Kis sugár}
FKi:= IKi; {Keringési idő}
Fr:=
Ir; {A
bolygó sugara}
FFi:= IFi; {Kezdő fázis}
FC:=
IC; {A
bolygó színe}
End;
Function TBolygo.GetKis:
Integer;
Begin
GetKis:= Round(A*FRk);
End;
Function TBolygo.GetNagy:
Integer;
Begin
GetNagy:= FRn;
End;
Procedure TBolygo.Hely;
Begin
Fx:= Xk+Round(FRn*Cos(FFi*Pi/180));
Fy:= Yk-Round(A*FRk*Sin(FFi*Pi/180));
End;
Procedure TBolygo.Show;
Begin
Hely; SetColor(FC);
SetFillStyle(1,Fc); FillEllipse(Fx, Fy, Fr, Fr);
End;
Procedure TBolygo.Hide;
Begin
Hely; SetColor(Uc);
SetFillStyle(1,Uc); FillEllipse(Fx, Fy, Fr, Fr);
End;
Procedure TBolygo.Mozgas;
Begin
Hide; FFi:= FFi+360/FKi; Show;
End;
Procedure TControl.Init;
Var Gd, Gm: Integer;
Begin
Gd:= InstallUserDriver('svga256',Nil); Gm:= 4; InitGraph(Gd,Gm,'');
Xk:= GetMaxX Div 2; Yk:= GetMaxY Div
2; SetFillStyle(1,Uc);
Bar(0,0, GetMaxX,
GetMaxY);
SetColor(15);
OutTextXY(Xk-50,0,'Naprendszer');
Nap.Init (
0, 0, 0, 7, 0,14); Nap.Show;
SetColor(14);
OutTextXY(Xk+12,Yk-3,'Nap');
Mercur.Init ( 61, 55,
88, 2, 90, 12);
SetColor(12);
OutTextXY(Xk-10,Yk+Mercur.GetKis+5,'Mercur');
Venus.Init (110,106,
224, 2, 90, 11);
SetColor(11);
OutTextXY(Xk-10,Yk+Venus.GetKis+5,'Venus');
Fold.Init (155,145,
365, 3, 90, 9);
SetColor(9);
OutTextXY(Xk-10,Yk+Fold.GetKis+5,'Fold');
Mars.Init (230,226,
684, 2, 90, 4);
SetColor(4);
OutTextXY(Xk-10,Yk+Mars.GetKis+5,'Mars');
Jupiter.Init
(290,280, 4330, 4, 90, 14);
SetColor(14);
OutTextXY(Xk-10,Yk+Jupiter.GetKis+5,'Jupiter');
Saturnus.Init(350,340,10752,
4, 90, 9);
SetColor(9);
OutTextXY(Xk-10,Yk+Saturnus.GetKis+5,'Saturnus');
Uranus.Init (400,390,30660, 3, 90, 10);
SetColor(10);
OutTextXY(Xk-10,Yk+Uranus.GetKis+5,'Uranus');
Neptunus.Init(450,440,60225,
2, 90, 11);
SetColor(11);
OutTextXY(Xk-10,Yk+Neptunus.GetKis+5,'Neptunus');
Pluto.Init (500,490,90520, 2, 90, 2);
SetColor(2);
OutTextXY(Xk-10,Yk+Pluto.GetKis+5,'Pluto');
End;
Procedure TControl.Run;
Begin
Repeat
SetColor(6); With
Mercur Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(3); With
Venus Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(9); With
Fold Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(5); With
Mars Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(7); With
Jupiter Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(8); With
Saturnus Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(1); With
Uranus Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(7); With
Neptunus Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
SetColor(8); With
Pluto Do
Begin
Mozgas; Ellipse(Xk, Yk, 0, 360, GetNagy, GetKis) End;
Until
KeyPressed;
End;
Procedure TControl.Done;
Begin
ClearDevice; CloseGraph;
End;
Var Control: TControl;
Begin
Control.Init;
Control.Run;
Control.Done;
End.
Készítsük el a következő zászlót:

Írjunk programot,
amely egy stadion képét jeleníti meg.
Például így:
